Основы векторного анализа цепей

Линейный измерения

4.1 Выполнение TOM калибровки

Калибровка это процедура, которая должна повторяться регулярно, делая конкретную последовательность работ чрезвычайно преимущественной. Для большинства новоприбывших специалистов калибровка выглядит как барьер для компетентных измерений. Чтобы помочь им преодолеть этот барьер, разделы 4.1 и 4.2 организованы в форме процедуры шаг за шагом, которые могут быть выполнены без чтения главы 3.

Испытательная установка:
◆◆ Векторный анализатор цепей,
◆◆ Два кабеля испытательных портов с разъемами PC3.5,
◆◆ Калибрационный набор системы PC3.5,
◆◆ Динамометрический ключ.

Процедура:
1. Подсоедините кабели испытательных портов к анализатору.

2. Для выполнения высоко прецизионных измерений, пожалуйста, зафиксируйте время прогрева анализатора (например, данное в листе спецификаций).

3. Сначала спланируйте предустановки канала, такие как стартовая и конечная частоты, число точек, тип качания (развертки), выходной уровень тестового порта и полосу пропускания измерений. Не откалиброванное пробное измерение, сделанное на фазе прогрева, может помочь в правильном выборе параметров.

4. Убедитесь, что калибровочный набор содержит правильные типы разъемов. Вы должны использовать те же типы разъемов, которые используются ИУ. Однако, существуют некоторые
   исключения: в случае ИУ с SMA разъемами используйте калибровочный набор PC3.5, поскольку разъем SMA типа не удобен для применения высокоточных калибрационных наборов. Он имеет те же самые опорные плоскости, что и разъем PC3.5. Убедитесь, что калибрационный набор походит для выбранного частотного диапазона измерений.

5. Калибрационный набор включает устройство запоминания, содержащее характеристические данные для калибрационных стандартов. Импортируйте данные внутрь анализатора.

6. Начинайте двух-портовую TOM калибровку. Выберите тип разъема для испытательных портов (в нашем случае PC3.5 (m)).

7. Если вы установили важные характеристические данные в процессе прежнего калибрационного процесса, достаточно только выбрать правильный набор данных. В этом случае запишите, что другие калибрационные наборы с тем же типом разъемов будут установлены на анализатор цепей. Убедитесь, что вы выбрали характеристические данные, которые вы прежде установили для разъема типа PC3.5 (m).

8. Теперь присоедините калибрационные стандарты один за другим к испытательным портам и выполните калибрационное измерение для каждого присоединенного стандарта. Чтобы предотвратить искажение измерения, не перемещайте испытательный кабель и стандарт в процессе этого измерения. Необходимое время качания зависит от числа точек и выбранной полосы пропускания измерения.

9. Как только вы измерили все существенные стандарты, анализатор цепей может определить коррекционные данные, используя соответствующую кнопку („Apply“). Прибор указывает, что он откалиброван, как только вычисления завершены, например путем метки „Cal“, указываемой в области диаграммы.

4.2 Выполнение TNA калибровки

TNA техника калибровки особенно хорошо подходит для измерений с использованием испытательных приспособлений. Первичный выигрыш этой техники калибровки лежит в минимальных требованиях, которые связаны со свойствами стандартов.

Испытательная установка
◆◆ Векторный анализатор цепей
◆◆ Два кабеля тестовых портов, соединенных с тестовым приспособлением
◆◆ Проходной (Т) стандарт, размещенный на подложке
◆◆ Стандарт аттенюатора (А), размещенный на подложке
◆◆ Стандарт симметричной цепи (N)1)

Процедура

1. Сначала новый калибрационный набор должен быть создан в анализаторе цепей. В некоторых случаях необходимо сначала определить также тип разъема. Назначьте имя, например, «Приспособление». В качестве рода разъема выберите «бесполый» (sexless). Теперь вы можете назначить новый калибрационный набор типу разъема «Приспособление», например, с именем
   TNAfix.

2. Теперь создайте TNA стандарт для калибрационного набора, как описано ниже. Убедитесь, что выбран тип разъема «Приспособление».

●● Определите проходной (Т) стандарт, введя его точную физическую длину и его потери.
●● Симметричная цепь (N), показанная на рис. 4.2.1, указана как приблизительно разомкнутая.
●● Стандарт аттенюатора (А) не требует каких-либо спецификаций.

3. Установите электрические соединения между испытательным приспособлением и анализатором цепей.
4. Как описывалось в разделе 4.1, выполните все установки канала и убедитесь, что принято во внимание время прогрева прибора.

5. Начинайте двух-портовую калибровку и используйте TNA процедуру калибровки. Выберите калибрационный набор TNAfix, который вы создали.

6. Внимательно вставьте аттенюатор (А) в испытательное приспособление. Зажмите приспособление. Убедитесь, что внутренний проводник расположен правильно. Выполните калибрационное измерение для аттенюатора (А). Разожмите испытательное приспособление и удалите стандарт.

7. Аккуратно вставьте стандарт симметричной цепи (N) (сформированный в этом случае подложкой без линии передачи) в испытательное приспособление. Действуйте, как описано в пункте 6 выше.

8. Аккуратно вставьте проходной переход (Т) в испытательное приспособление и действуйте, как описано в пункте 6 выше.

9. Если вы располагаете короткозамыкателем, вы можете его использовать для верификации результатов. Однако эта верификация имеет свои ограничения.

4.3 Измерение коэффициента отражения и КСВ

Измерения коэффициента отражения выполняются иногда на одно-портовых устройствах. Одно-портовое ИУ имеют только одну пару выводов, так что достаточно провести одно-портовую калибровку (OSM калибровку). Когда необходимо определить коэффициент отражения двух-портового устройства, требуется двух-портовая калибровка. Оба порта ИУ должны быть соединены с анализатором цепей. В качестве общепринятого правила N портовое ИУ требует N-портовой калибровки.

Диаграмма Смита является наиболее общей из известных для проектирования простых согласующих цепей. Все параметры, необходимые для этих цепей, могут считываться непосредственно, используя графическую технику проектирования. Детальное описание этого здесь не приводится. Это часть почти всех вводных книг по СВЧ технике. Диаграмма Смита также подходит для идентификации компонентов. На следующих двух диаграммах Смита показаны графики коэффициента отражения для типовых одно-портовых устройств. Эти диаграммы были нормированы к опорному импедансу Z0 = 50 Ω. графики генерировались как результат частотного качания, выполнявшегося анализатором цепей. Их не следует путать с траекториями преобразования, например, используемыми в [MG92] для определения согласующей цепи.

Резистор со значением 10 Ω приводит к частотно-независимой точке z = 0,2, показанной зеленым цветом на рис. 4.3.1. Для f = 0 Гц индуктивность L = 100 нГн ведет себя, как нагрузка КЗ. При возрастании частоты мнимая часть импеданса растет (красная кривая на рис. 4.3.1). На финальной частоте 100 МГц она достигает точки z = 1,26j. Если мы присоединим резистор 25 Ω последовательно с индуктивностью, мы получим график, показанной, оранжевым цветом на
рис. 4.3.1. На финальной частоте последовательная цепь достигает точки z = 0,5 + 1,26j. Конденсатор емкостью 40 пФ ведет себя, как нагрузка ХХ на частоте f = 0 Гц. То же самое относится к последовательной цепи, состоящей из конденсатора и резистора. С возрастанием частоты мнимая часть импеданса конденсатора предполагается имеющей конечные значения. Они имеют отрицательный знак. Частотно-зависимый импеданс конденсатора (или импеданс последовательной цепи, состоящей из конденсатора и резистора) показан на рис. 4.3.1 как темно-голубой (или светло-голубой) график. Особенно на высоких частотах эффекты потерь, а также эффекты паразитных резонансов в компонентах приводят к отклонению от графика, показанных на рис. 4.3.1.

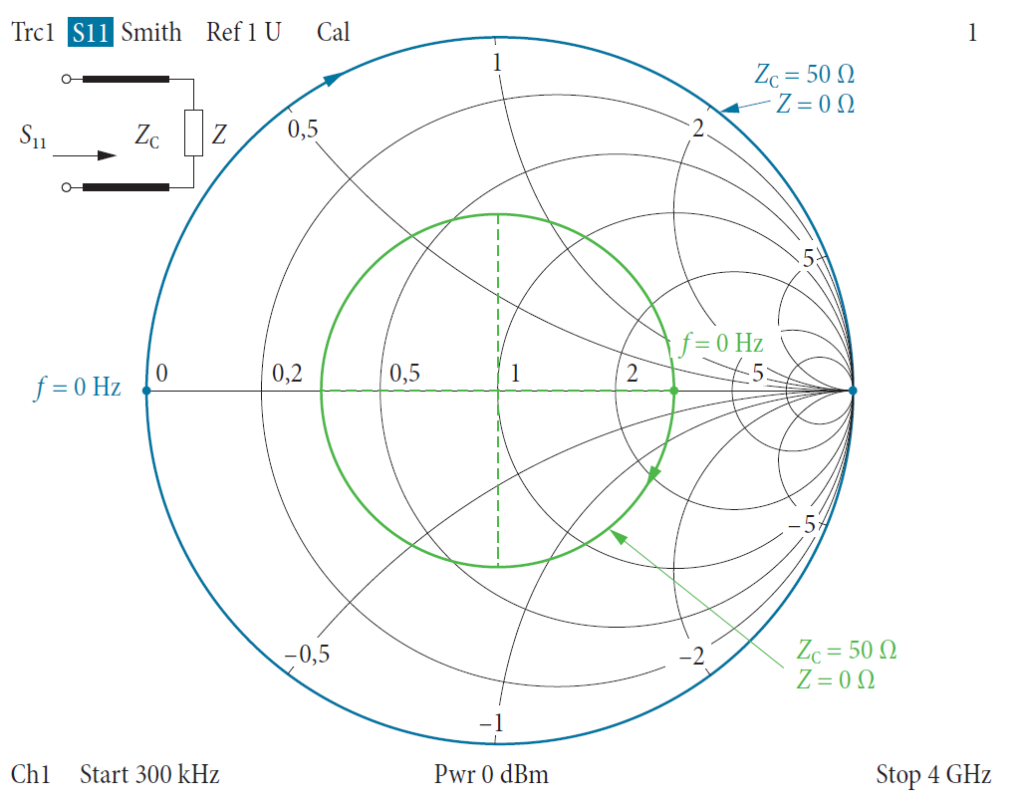
Рис. 4.3.2 показывает коэффициента отражения по входу различных конфигураций линий передачи. Линии передачи с характеристическим импедансом ZC и импедансом нагрузки Z считаются однородными и приблизительно без потерь. В первом случае линия передачи с Z = 50 Ω оканчивается нагрузкой КЗ Z = 0 Ω. График начинается от 0 Гц при z = 0. С возрастанием частоты она пробегает вдоль внешней окружности на диаграмме Смита (голубой цвет на рис. 4.3.2). Центральная точка окружности лежит в точке нормированного импеданса z = ZC/50 Ω = 1. Если мы оканчиваем такую же линию передачи импедансом Z = 150 Ω, то график при 0 Гц будет начинаться в точке z = 3. Подобно предыдущему случаю, мы опять замечаем кривую окружности вокруг точки z = 1 с тем же направлением вращения (зеленый график на рис. 4.3.2). В случае линий передачи с потерями возникают кривые спиральной формы, и график имеет тенденцию с возрастанием частоты сходиться к точке s11 = 0 (соответствующей z = 1 + 0j).

Чтобы проконтролировать согласование высококачественного фиксированного аттенюатора в большинстве случаев будет достаточно модуля коэффициента отражения. Более того, диаграмма Смита не очень удобна для малых коэффициентов отражения из-за ее линейной шкалы. Полезно сформатировать коэффициент отражения s11 как децибельное (дБ) значение и показать его на декартовой диаграмме. Преобразованный коэффициент отражения называется
отражением. Типичный пример это отражение as11, вычисленное из коэффициента отражения s11:

Благодаря падающей волне a и отраженной волне b вдоль линии передачи формируется картина суперпозиции. Мы можем различать три различные картины:

◆◆ Если линия передачи заканчивается при |Г| = 1, то возникает картина стоячей волны. Никакой энергии не передается вдоль линии передачи. Огибающая колебания имеет фиксированные узлы, где Umin = 0.

◆◆ Если линия заканчивается с |Г| = 0, никакого взаимодействия не возникает, поскольку b = 0. Формируются только бегущие волны, а стоячие волны отсутствуют. Огибающая не имеет никаких узловых точек. Она имеет одно и то же напряжение Umin = Umax при любом расположении.

◆◆ В процессе нормальной работы часть энергии отражается от нагрузки. Используя пробник напряжения, можно измерить напряжения Umin и Umax огибающей.

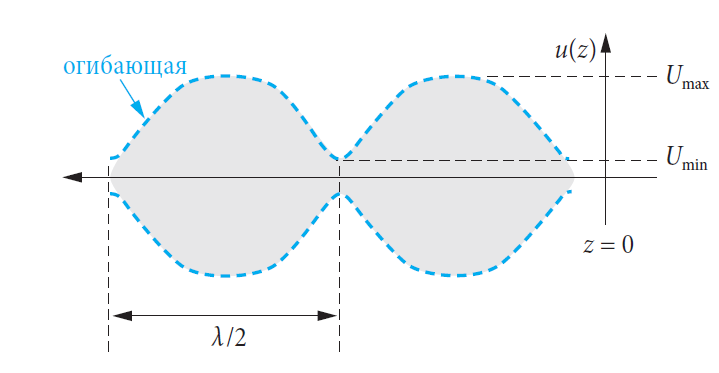
Коэффициент стоячей волны или коэффициент стоячей волны по напряжению (КСВ или КСВН) это отношение максимума Umax к минимуму Umin. Однако, измерения пробником напряжения требуют очень много времени и относительно неточны. С другой стороны, анализатор цепей вычисляет коэффициент стоячей волны, например, в тестовым порту 1, из модуля |s11| коэффициента отражения.

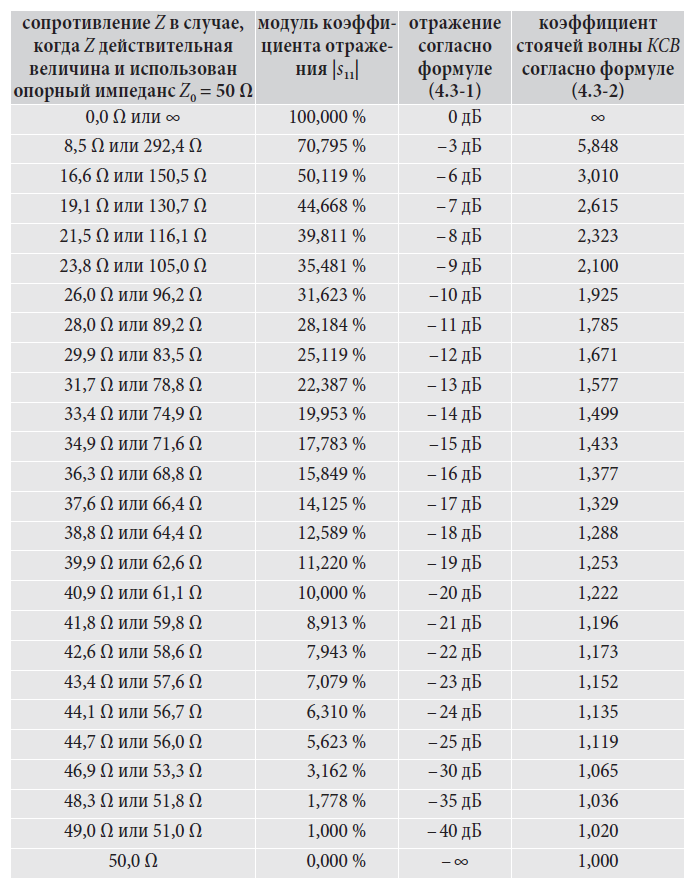
Чтобы показывать коэффициент стоячей волны, просто выберите формат КСВ (SWR) на анализаторе цепей. Следующая таблица преобразований показывает соотношение между четырьмя величинами Z, s11, as11 и КСВ.

4.4 Измерение коэффициента передачи

При измерении коэффициента передачи первым делом необходимо выполнить калибровку, например, как описано в разделах 4.1 или 4.2. Для грубой оценки модуля мы можем это выполнить без предварительной калибровки. В этом случае график обычно содержит
наложенные пульсации, и для кабелей тестовых портов следует ожидать потери (например, от 1 дБ до 3 дБ для 1 м кабеля на частоте 8 ГГц).

Для пассивного ИУ модуль коэффициента передачи будет иметь значения в диапазоне от 1 (идеальный проходной переход) до 0 (нет соединения). Коэффициенты передачи обычно показываются в формате дБ по модулю.

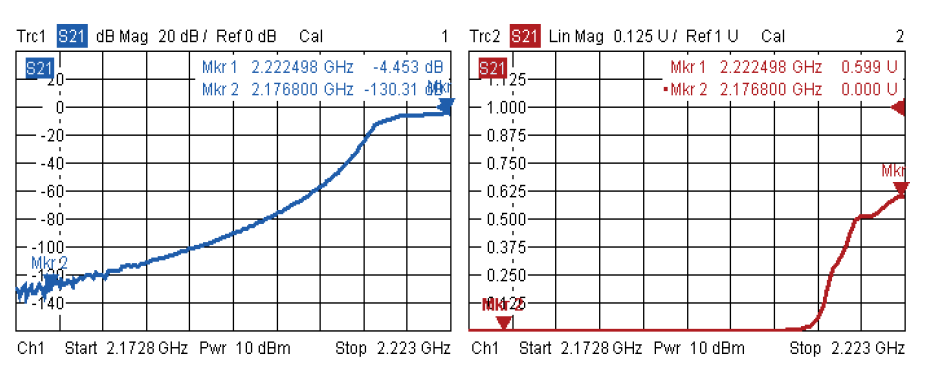
Преимущество логарифмической шкалы заключается в том, что она предлагает возможность считывать очень малые коэффициенты передачи, такие как s21 = 10–8, что соответствует a21 = –160 дБ, с большой точностью. В то же самое время, эта шкала позволяет указывать большие значения, такие как s21 = 100, что соответствует as21 = 40 дБ на этой же диаграмме. Поэтому логарифмическая шкала лучше подходит для измерений, чем линейная шкала. Рис. 4.4.1 иллюстрирует это, используя пример фильтра с высокой полосой пропускания. В левой части рисунка используется шкала в дБ, а в правой части – линейная шкала. Передача as21 = 0 дБ соответствовала бы идеальной полосе пропускания. Из-за потерь в фильтре рис. 4.4.1 показывает вносимые потери 4,4 дБ. В диапазоне режекции фильтра его порты развязаны. Здесь нет соединения. Это соответствует передаче as21 = ∞. На самом деле порты фильтра не полностью развязаны, так что мы можем ожидать конечного значения для as21. Минимальный уровень шума приемников и изоляции тестовых портов анализатора ограничивают нашу возможность верификации этого значения. Предел зависит от свойств анализатора цепей и его установок; на рис. 4.4.1 от равен приблизительно –130 дБ.

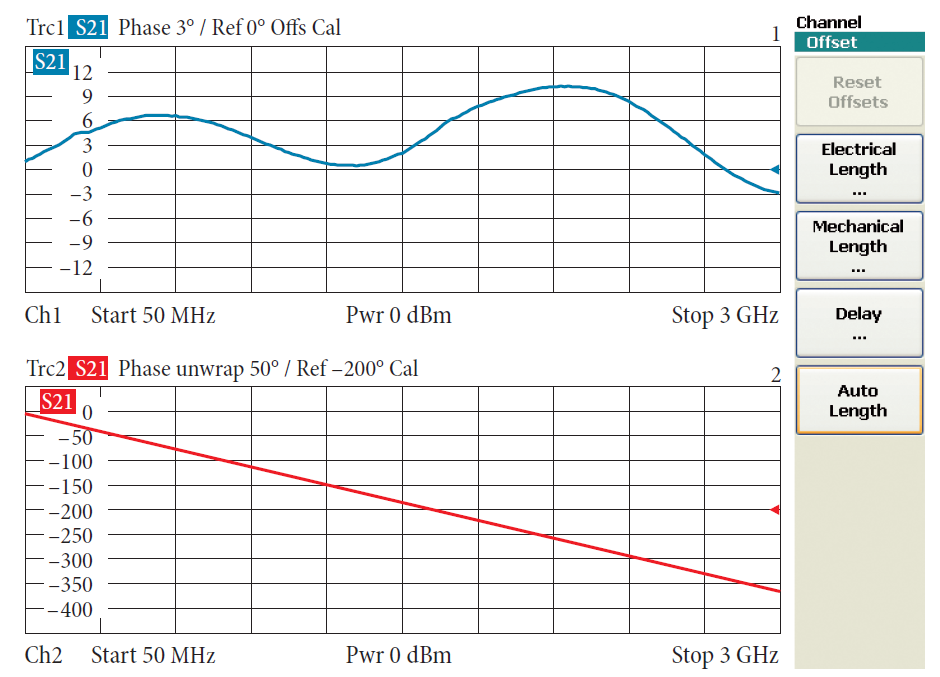
В некоторых случаях необходимо также указывать фазу коэффициента передачи. В этом случае коррекция системной ошибки крайне необходима. Значения фазы строятся в градусах в функции от частоты. Значения фазы обычно сосредоточены в диапазоне от –180° до 180°. Если вам необходимо исследовать фазу в непосредственной близости от этих пределов, вы можете непрерывно указывать фазу, используя формат развернутой фазы. Рис. 4.6.2 показывает сравнение между индикацией нормальной фазы и нерасщепленной фазы.

4.5 Измерение группового запаздывания

Групповое запаздывание (задержка) τгр рассчитывается из коэффициента передачи, например, s21.

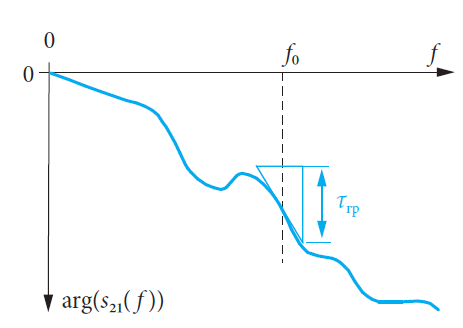
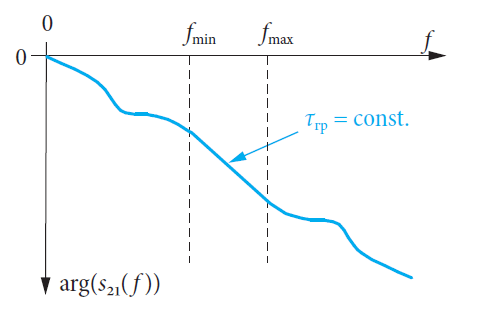
Групповое запаздывание τгр( f0) соответствует наклону фазы arg(s21( f0)) в функции от частоты f0. Этот наклон масштабирован по коэффициенту –1/(2π) или –1/360°, что приводит к тому, что физической единицей групповой задержки является секунда (с):

Двух-портовая цепь свободна от линейных искажений в частотном диапазоне от fmin до fmax, если она удовлетворяет следующим требованиям в этом частотном диапазоне:
◆◆ Постоянная групповая задержка τгр( f ) (см. рис. 5.4.1б) и
◆◆ Постоянный модуль коэффициента передачи |s21( f )|.

При этих условиях групповая задержка τгр является мерой того, насколько долго требуется модуляционным компонентам сигнала с несущей частотой fmin < f < fmax для распространения через цепь. Эта компоненты могут наблюдаться во временной области как график огибающей модулированного сигнала.

Графики, показанные на рис. 4.5.1a/б, основаны на алгебраических выражениях типа s21( f ) = 0,5 ∙ fц2/( fц2 – f 2 + jBf ), которые могут быть прямо вставлены в формулу (4.5.1) и производная (частное от дифференциалов d/df ) может быть взята путем алгебры. В отличие от этого анализатор цепей измеряет S-параметры на оси дискретных частот. Эта частотная ось имеет размер шага Δf, подобный тому, который обозначен на рис. 4.5.2. Поэтому производная d/df может быть аппроксимирована численно как отношение разностей.

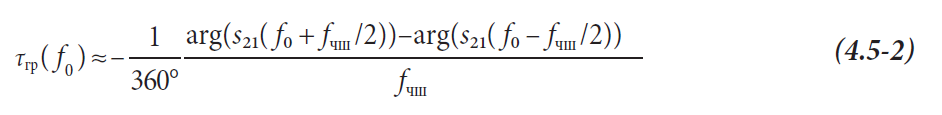
Для большей гибкости полезно различать Δf и размер частотного шага fчш = kΔf, который используется для расчета частного разностей. Обычно это называется апертурой. Коэффициент k называется шириной шага апертуры.

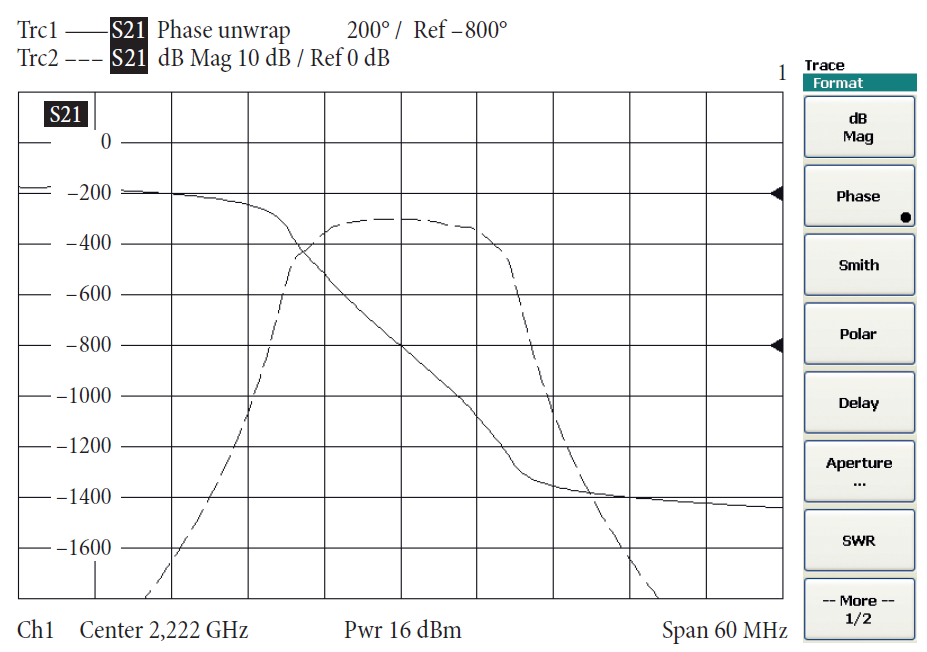
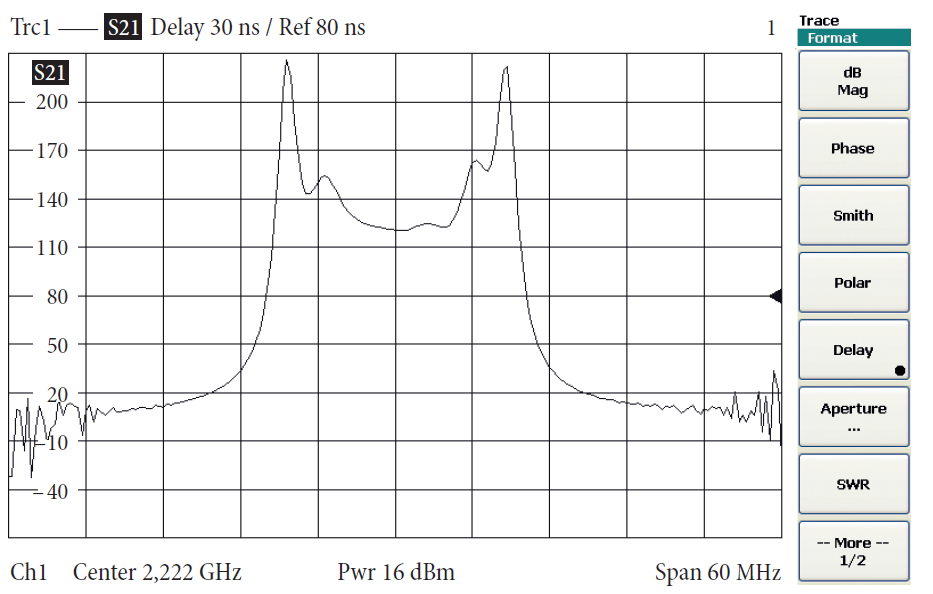
В следующем примере измерялся полосовой фильтр. Рис. 4.5.3 показывает соответствующие графики фазы и модуля для коэффициента передачи s21. На рис. 4.5.4–4.5.6 изменялась ширина шага апертуры k. В настоящем примере ширина шага апертуры k = 10 соответствует хорошему выбору. Документация по измерению группового запаздывания включает апертуру fчш, которая реально используется. Шум, который внутренне присутствует при любых измерениях, расширяет измеренное групповое запаздывание. Например, уменьшая полосу пропускания по ПЧ, можно снизить шум, накладываемый на S-параметр, и таким образом снизить шум графики
группового запаздывания.

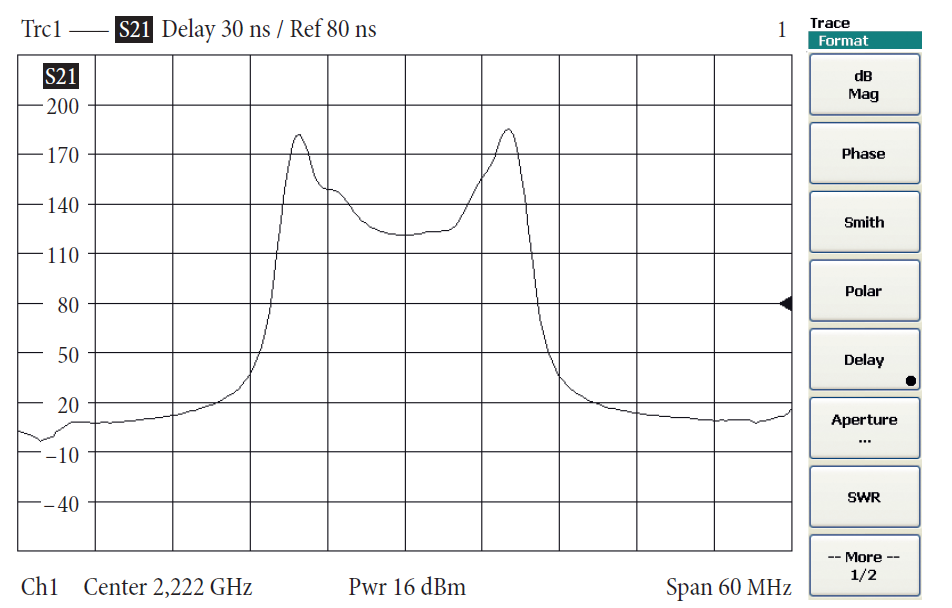
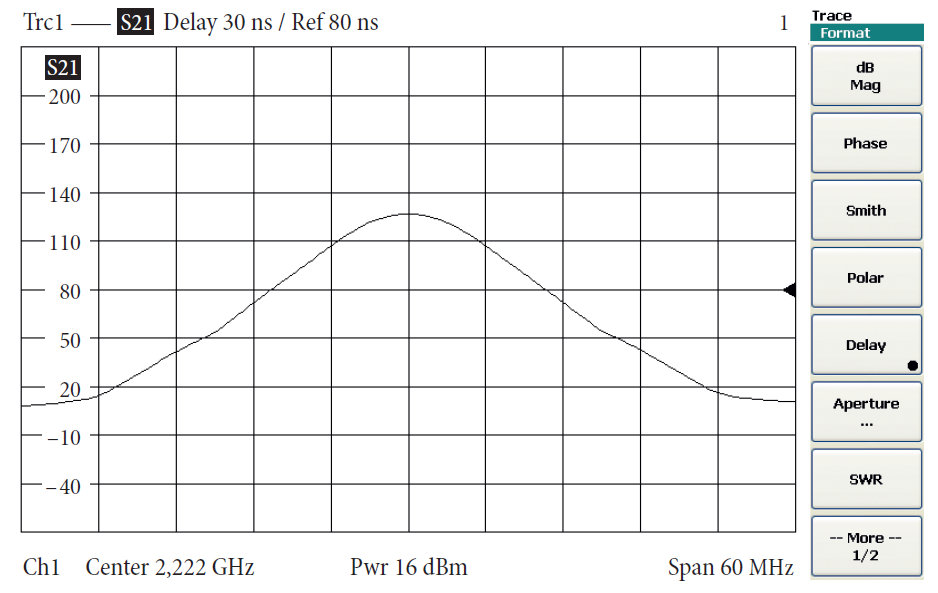
4.6 Измерение фазового запаздывания, автоматической длины

Фазовое запаздывание является функцией абсолютной фазы на частоте f. Обычно оно рассчитывается из коэффициента передачи, например, s21.

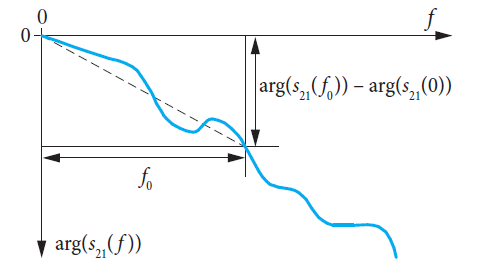
Фазовое запаздывание τФ( f ) пропорционально диапазону фазы, расположенному между 0 Гц и интересующей частотой f, разделенному на интересующую частоту. При этом вычислении фаза при 0 Гц предполагается равной 1) arg(s21(0 Гц)) = 0.

1) Это также применимо в случае, когда цепь (например, двух-портовая цепь) имеет коэффициент передачи s21 = 0 для f = 0, так что значение фазы arg(s21(0)) при f = 0 было бы, строго говоря, неопределенным.

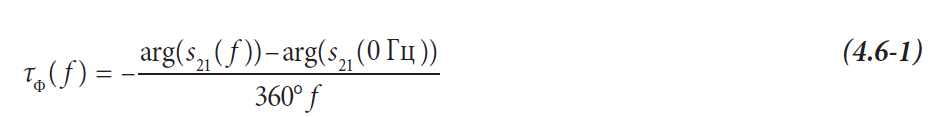
В цепях, не имеющих искажений и дисперсии, фазовое запаздывание остается постоянным, характерным для этой цепи. Это значение дает временное запаздывание в секундах, испытываемое всеми синусоидальными компонентами, когда они проходят через цепь.
Таким образом, фазовое запаздывание сильно связано с длиной линий передачи. Типовые линии передачи демонстрируют фазовую задержку от нескольких пикосекунд до нескольких наносекунд для длинных линий. Электрическая длина lэл линий передачи может быть рассчитана, например, из скорости света в вакууме c0 = 2,99792458 ∙ 108 м/с и фазовой задержки τФ.

В случае гомогенной (однородной) линии передачи примерно без потерь мы можем рассчитать фазовое запаздывание из механической длины lмех и относительной диэлектрической проницаемости εr диэлектрика следующим образом:

Анализаторы цепей типично используют следующую формулу для определения фазового запаздывания. Она отличается от определения в формуле (4.6-1) использованием стартовой частоты fstart вместо частоты 0 Гц.

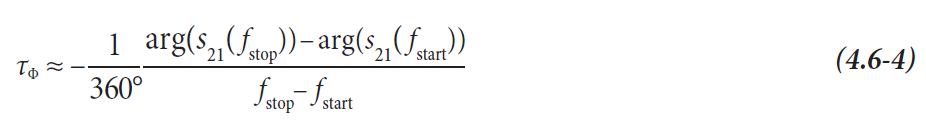
Величины fstart и fstop обозначают начальную и конечную частоты выбранного диапазона частотного качания. Некоторые анализаторы цепей также обеспечивают возможность использовать меньший сегмент графика вместо полного диапазона качания (см. нижнюю часть рис. 4.6.2 с сегментом графика от 1 ГГц до 2 ГГц).

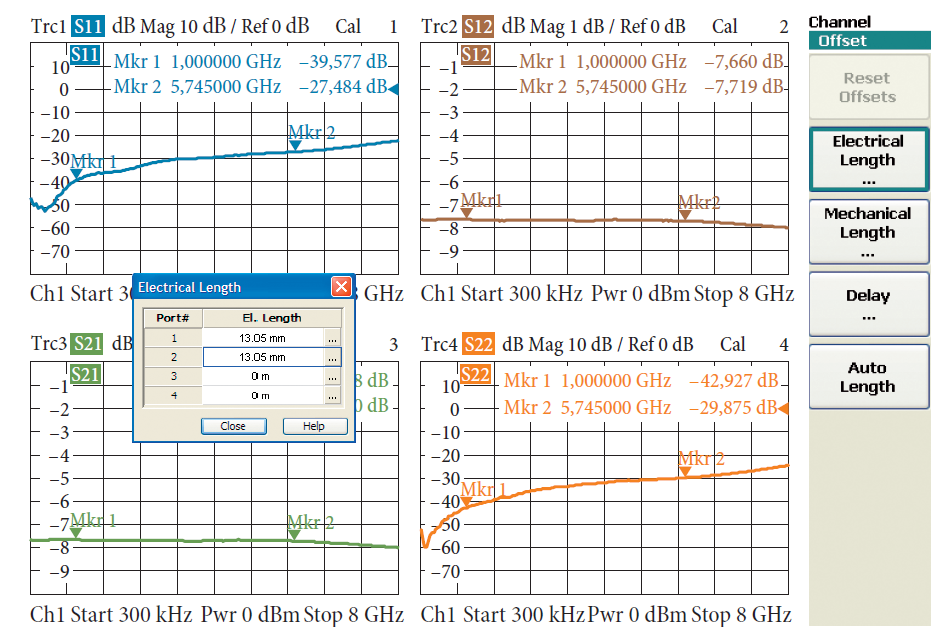
Функция автоматической длины вычисляет среднюю электрическую длину loffs во всем диапазоне качания. Анализатор цепей использует это смещение длины для коррекции последующих измерений. Автоматическая длина была активирована для верхнего графика на рис. 4.6.3. В результате график показывает отклонение от линейной фазы. Если смещение длины не вычитается, то эти отклонения не могут быть приняты в большинстве случаев (см. нижний график на рис. 4.6.3).

4.7 Измерение устойчивости

Неустойчивость есть фундаментальная угроза для любого усилителя. В неустойчивом состоянии усилитель действует, как генератор, и будет вырабатывать (нежелаемый) выходной сигнал, даже если никакого входного сигнала не присутствует. В других участках частотного диапазона неустойчивость будет снижать усиление в большинстве случаев.

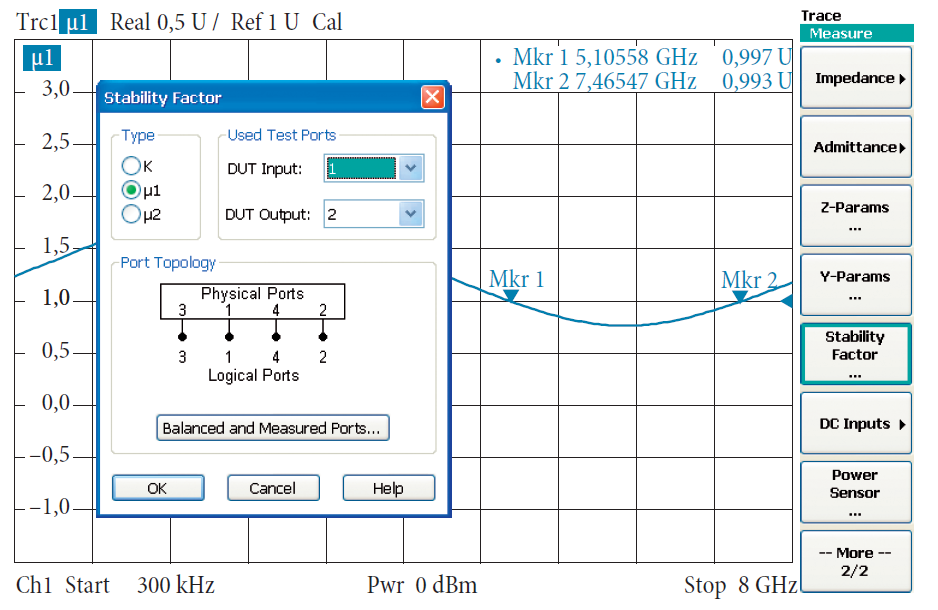
Линейную схему, которая является устойчивой при любых пассивных конфигурациях на входе и выходе, называют безусловно устойчивой. Все цепи с коэффициентом отражения |Г|<1 рассматриваются как пассивные. Чтобы оценивать устойчивость линейного двух-портового устройства, мы можем использовать коэффициенты устойчивости μ1 или μ2, известные из литературы [ES92]. Анализатор цепей вычисляет их из четырех комплексных S-параметров двухпортового устройства и показывает их как функции от частоты и некоторых других воздействующих величин.

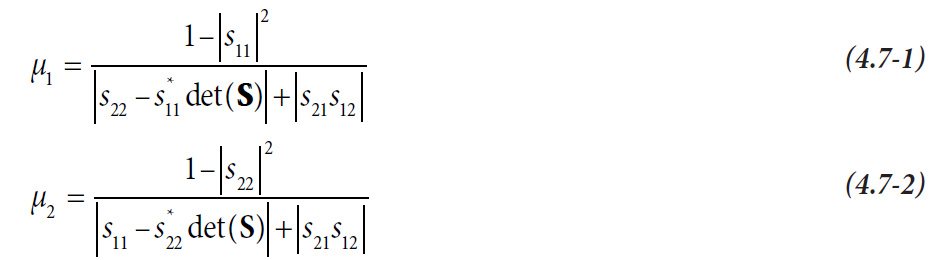
Необходимый и достаточный критерий безусловной устойчивости линейного двух-портового устройства это условие μ1 > 1. Как альтернативу, можно также контролировать, что μ2 > 1. Многие анализаторы цепей обеспечивают только коэффициент устойчивости k, описанный Ролле (Rollet) [Ro62] для использования в исследовании устойчивости.

В технической литературе этот коэффициент гораздо более известен, чем коэффициенты μ. Однако условие k > 1 является необходимым, но не достаточным для безусловной устойчивости. Мы должны добавить одно из следующих дополнительных условий, чтобы получить необходимый и достаточный критерий.

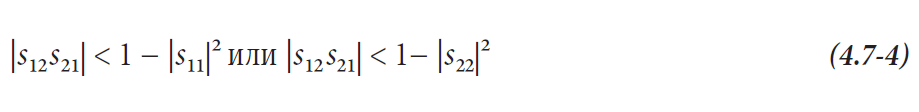
Все коэффициенты устойчивости, описанные здесь, являются действительными величинами. Они обычно индицируются на линейной шкале (формат: Real). Рис. 4.7.1 ниже представляет анализ устойчивости, используя коэффициент устойчивости μ1. В частотном диапазоне между маркерами 1 и 2 усилитель не является безусловно устойчивым. В большинстве случаев можно найти некоторые специфические конфигурации на входе и выходе, для которых усилитель демонстрирует устойчивое поведение. Для этих конкретных значений Г, наблюдаемых на входе и выходе, говорят, что усилитель является условно устойчивым. Но на практике мы обычно
предпочитаем безусловно устойчивые усилители.

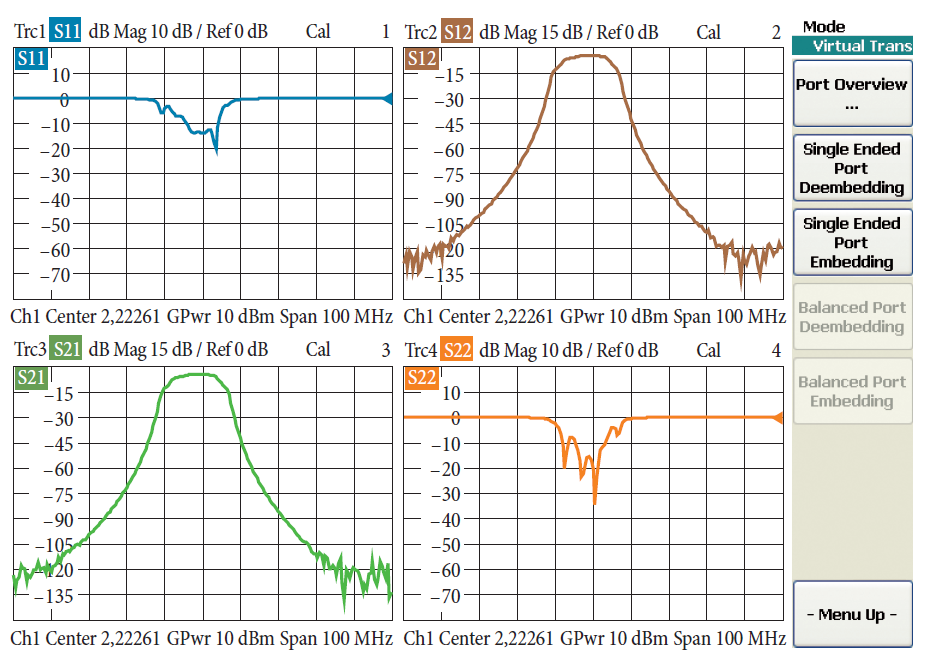
4.8 Измерение со внедрением виртуальных цепей (Embedding)

При внедрении виртуальных цепей измеряется компонент, как если бы он был встроен в определенную (но не физически присутствующую) среду цепи. Среда цепи этого типа известна как виртуальная цепь трансформации. Типичные примеры это согласующие цепи для усилителя или конструкции эквалайзера (выравнивающего устройства) для фильтра (оба определяются, например, используя программу автоматизированного проектирования CAD).

Все, что физически присутствует в этих примерах, это усилитель или фильтр.

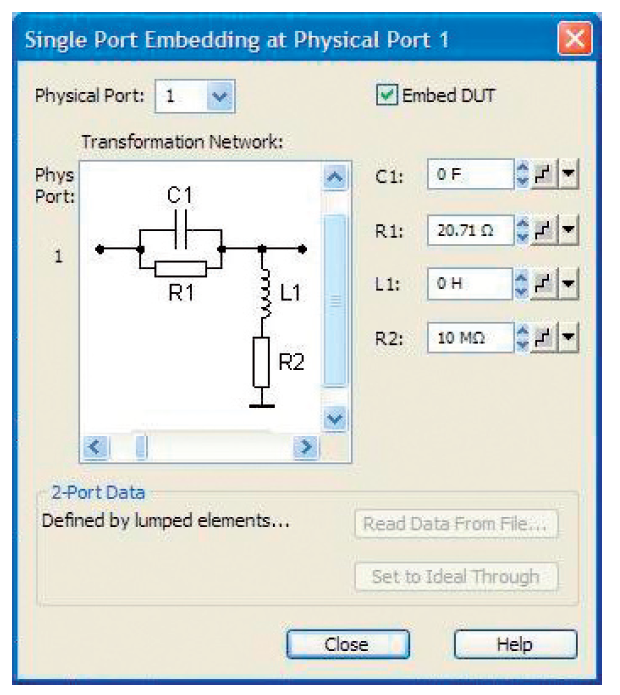
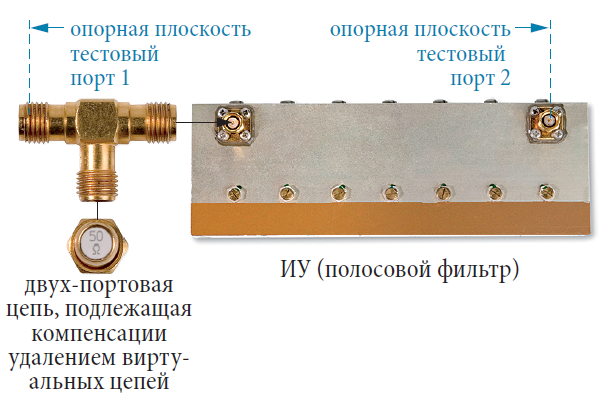
Рисунок ниже показывает цепь для фиксированного Т-образного аттенюатора. Он дает ослабление 7,7 дБ и все порты являются согласованными s11 = s22 = 0.

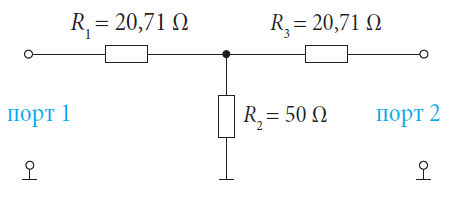
Для целей иллюстрации резисторы R1 и R2 реализованы через внедрение виртуальных цепей. ИУ, которое физически присутствует, состоит только из Т-перехода и резистора 50 Ω (см. рис. 4.8.2). Разъемы Т-перехода формируют внутренние порты. Однако после внедрения результаты измерений должны быть отнесены к виртуальным тестовым портам 1 и 2.

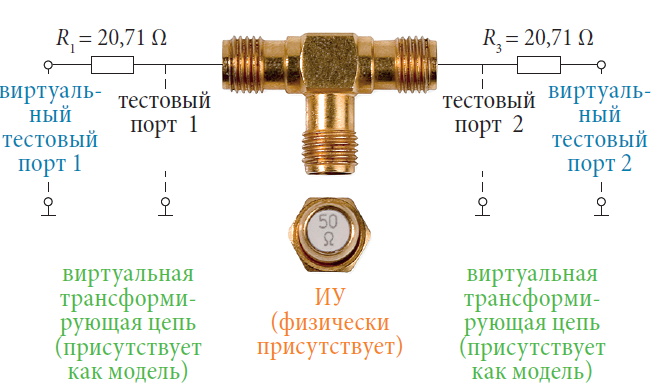
Как первый шаг, выполняется двух-портовая калибровка, например, использующая технику ТОМ. Это является основным требованием для внедрения виртуальных цепей. Измеряются все четыре S-параметра двух-портовой цепи, состоящей из Т-перехода и резистора 50 Ω (см. рис. 4.8.3). Измеряется ослабление 3,5 дБ. Поскольку резисторы R1 и R3 все еще опускаются, неполный фиксированный аттенюатор показывает относительно худшие обратные потери
9,5 дБ.

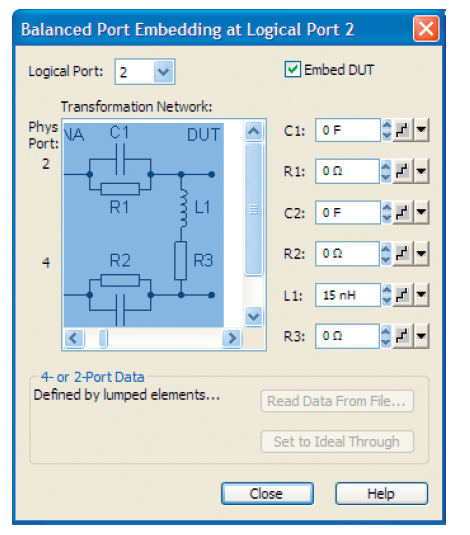
Наш пример особенно удобен для использования параметризованной модели цепи (см. рис. 4.8.4). Встроенный последовательный резистор установлен на 20,71 Ω. Все другие встроенные компоненты установлены на нейтральные значения (C1 = 0 Ф, L1 = 0 Гн, R2 = 10 МΩ). Внедрение виртуальных цепей может быть включено и отключено, используя клавишу „Embed DUT“ (встроенное ИУ). Такая же ситуация по входу выполнена по второму тестовому порту.

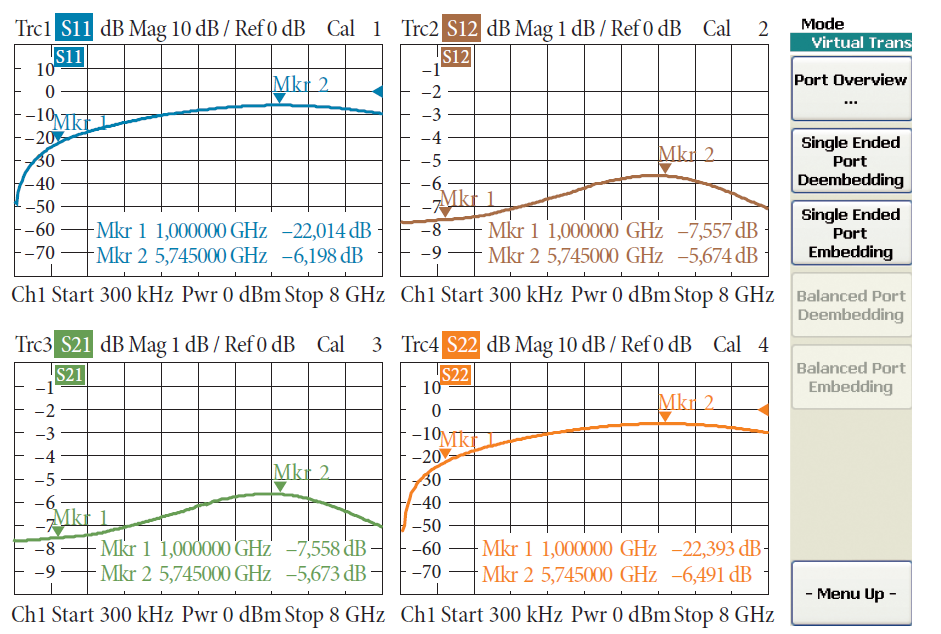
После встраивания измеряются S-параметры, показанные ниже, для полной схемы между виртуальными тестовыми портами 1 и 2 (сравни с рис. 4.8.2).

Для частот вплоть до 1 ГГц результаты измерений соответствуют ожиданиям. По умолчанию, последовательные резисторы R1 и R3 предполагаются расположенными в опорной плоскости калиброванного анализатора цепей. Как можно заключить из рис. 4.8.6, эта плоскость располагается внутри разъема. Между резисторами R1 и R3 и узловой точкой Т-перехода есть отрезки линии передачи l1 и l2, соответственно. Обе длины показаны на рис. 4.8.6 ниже. Отрезок линии с длиной l2 оканчивается последовательной цепью из R3 и виртуального тестового порта 2 (см. рис. 4.8.2). Импеданс этой последовательной цепи равен примерно 70 Ω. Другими словами, этот отрезок линии не оканчивается характеристическим импедансом Zc = 50 Ω. Это означает, что это вызывает частотно-зависимую трансформацию, которая оказывает влияние на все четыре S-параметра на рис. 4.8.5. Это же самое применимо к другому отрезку линии, которая соединена с импедансом источника R1 + 50 Ω ≈ 70 Ω.

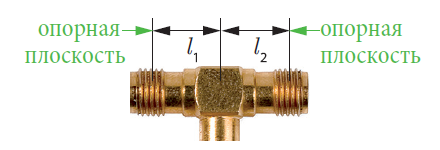
Выбирая подходящее смещение длины в тестовых портах 1 и 2, можно сдвинуть опорную плоскость внутрь Т-перехода. В настоящем случае мы можем определить это смещение длины следующими рассуждениями: на частоте 5,745 ГГц (соответствующей длине волны λ = 52,22 мм) параметр s имеет максимум. На этой длине волны предварительно рассчитанное рассогласование 70 Ω трансформируется отрезком линии l в минимум. Реальная трансформация основывается на предположении об электрической длине l = λ/4. Электрическая длина, требуемая для компенсации, равна поэтому l = 52,22 мм/4 = 13,05 мм. Из-за симметрии это значение удобно выбрать для обоих испытательных портов l = l . Результаты измерений из рис. 4.8.7 соответствуют нашим ожиданиям.

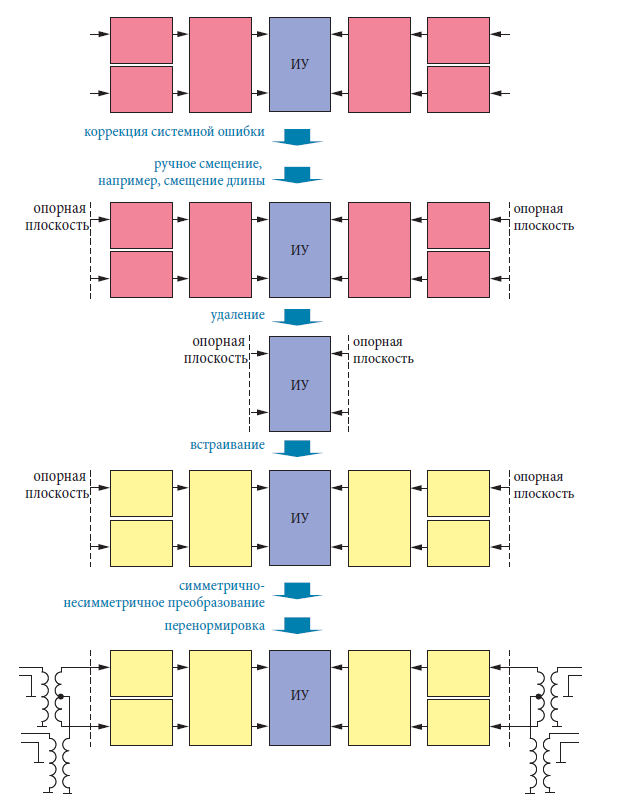
Внедрение виртуальных цепей с простыми моделями цепей или с S-параметрами (файлы *.s2p-, *.s4p) может быть скомбинировано с дополнительными механизмами. Возможности включают:

◆Учет виртуальных трансформаторов импеданса или изменение опорного импеданса до значения, которое расходится с физическим значением прибора, которое обычно равно Z = 50 Ω или Z = 75 Ω. Эта процедура известна как перенормировка S-параметров.
◆ Добавление отрезков однородных линий передачи смещением длины. Отрицательное смещение длины loffs < 0 добавляет виртуальный отрезок линии к цепи, в то время как положительное смещение длины компенсирует отрезок линии, который физически присутствует. Последнее описывается в следующем разделе («удаление виртуальных цепей»).

При использовании этих дополнительных механизмов важно принимать во внимание порядок индивидуальных шагов в цепочке вычислений анализатора цепей. Это показано на рис. 4.8.8 для семейства приборов, которое используется в этой книге. Техники невстраивания и симметрично-несимметричного преобразования включены для сохранения полноты и описываются разделами 4.9 и 4.10, соответственно.

4.9 Измерение с удалением виртуальных цепей

Намерение удаления виртуальных цепей это измерять ИУ, которое встроено в среду физической цепи, несмотря на то, имеет ли эта среда возможность математического удаления из результатов измерений. Например, ИУ может быть монолитной интегральной схемой СВЧ (microwave monolithic integrated circuit – MMIC), которая заключена в пластмассовый корпус. При измерении мы хотели бы получить данные самого кристалла без корпуса. Другими словами, не существует способа прямого доступа к виртуальным портам ИУ, которые нас интересуют. Предположим, что мы знаем части цепи Tч1 и Tч2, которые присутствуют между анализатором цепей и ИУ.

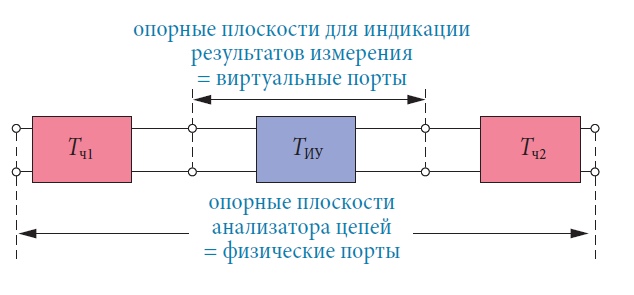
Полное характеризование цепей Tч1 и Tч2 обеспечивается анализатором цепей. Методы характеризования, используемые здесь, знакомы из встраивания (раздел 4.8). Анализатор вычисляет трансформацию, которая может быть использована для компенсации физически присутствующих цепей Tч1 и Tч2. Как только включается невстраивание, пользователь может воспользоваться преимуществами всех S-параметров, связанных с измеряемыми величинами,
диаграммами и форматами, доступными в приборе, как будто ИУ измерялся на его виртуальных тестовых портах.

Для целей иллюстрации мы будем использовать Т-переход с резистором 50 Ω как нашу цепь Tч1. Его S-параметры известны из рис. 4.8.3 и были экспортированы как *.s2p файл в формате Touchstone®. Мы не будем использовать цепь Tч2. Полосовой фильтр используется как ИУ. На калиброванном анализаторе цепей мы загружаем Т-переход с резистором 50 Ω, присоединенный к тестовому порту 1. За этим следует ИУ и тестовый порт 2.

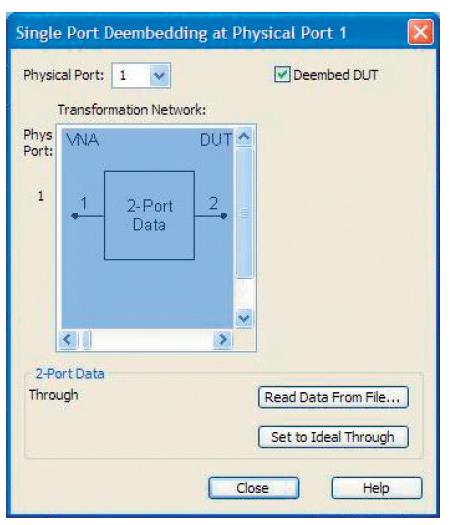
Здесь удаление виртуальных цепей необходимо только в тестовом порту 1. Характеризование цепи Tч1 проводится, как показано на рис. 4.9.3. Для этой цели загружаются соответствующие файлы *.s2p. В дополнение удаление в тестовом порту 1 может включаться и выключаться, используя клавишу „Deembed DUT“.

Как результат удаления виртуальных цепей, S-параметры полосового фильтра индицируются, как если бы цепь Tч1 не присутствовала.

Теперь мы будем модифицировать Т-переход, чтобы проиллюстрировать пределы удаления. Вместо резистора 50 Ω мы присоединяем стандарт ХХ (например, из калибрационного набора). Т-переход, который модифицируется в такой манере, сначала обмеряется один как двухпортовое устройство. Соответствующие S-параметры сохраняются в файле *.s2p. Их можно наблюдать на рис. 4.9.5. Мы можем видеть полюс на 4,22 ГГц. На этой частоте линия, идущая
от узловой точки Т-перехода, к ХХ, действует как шлейф λ/4. Соответствующая длина состоит из электрической длины ХХ и отрезка линии внутри Т-перехода. На частоте 4,22 ГГц линия действует как λ/4-трансформатор и трансформирует ХХ в КЗ. Этот КЗ соединен параллельно тестовым портам 1 и 2 и предотвращает передачу между двумя портами. Как следствие, коэффициенты передачи вперед и назад имеют полюс на этой конкретной частоте (см. также s12 и s21 на рис. 4.9.5).

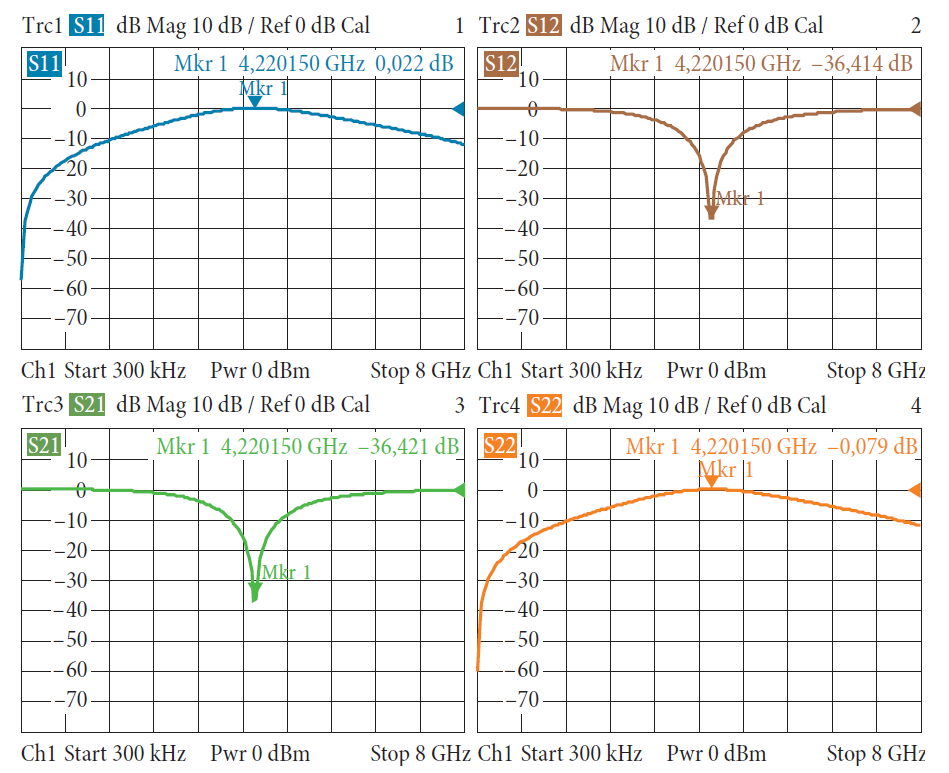
Цепь теперь расширена, чтобы включить ИУ (в данном случае фиксированный аттенюатор на 10 дБ). Он вставляется между модифицированным Т-переходом и тестовым портом 2. Файл *.s2p, связанный с рис. 4.9.5, назначается как невстраиваемая цепь к тестовым порту 1 анализатора. Результаты измерений с невстраиванием демонстрируют существенное отклонение на частоте 4,22 ГГц (см. рис. 4.9.6). Как описывалось ранее, на этой частоте передача через цепь Tч1 является невозможной. Измеренные значения a1 и b1 в тестовом порту 1 поэтому не содержат никакого сигнала, который позволил бы нам делать заключения об отражении от ИУ. Мы можем выполнить подобный анализ относительно передачи на частоте 4,22 ГГц. В окрестности этой частоты анализатор цепей не способен вычислять S-параметры ИУ, составленного как фиксированный аттенюатор на 10 дБ, из измеренных значений.

4.10 Измерение симметричных линий

При передаче сигналов по линиям передачи мы хотели бы уменьшить внешние помехи. Тем не менее, внешние нежелательные сигналы могут проникать, даже когда используется замкнутое экранирование, например, из-за конечной проводимости заземляющего проводника. Если мы передаем сигнал по паре симметрично связанных проводников, мы можем ожидать проникновение помех в обе линии в равной степени. С другой стороны, если мы вводим
желательный сигнал в один проводник с нулевой фазой, и в другой проводник со сдвигом фаз 180°, очень легко различить возникающий дифференциальный сигнал от помех синфазного режима. Эта конфигурация известна как симметричная (балансная)1) линия передачи. Идеальная конфигурация использует линию передачи типа витая пара без опорного заземления. В реальной жизни, однако, заземление обычно присутствует в окрестности линии, так что кроме желаемого сигнала дифференциального режима вдоль линии передачи может также распространяться сигнал синфазного режима. Что тут нежелательного, так это преобразование сигналов между синфазным и дифференциальным режимом, поскольку
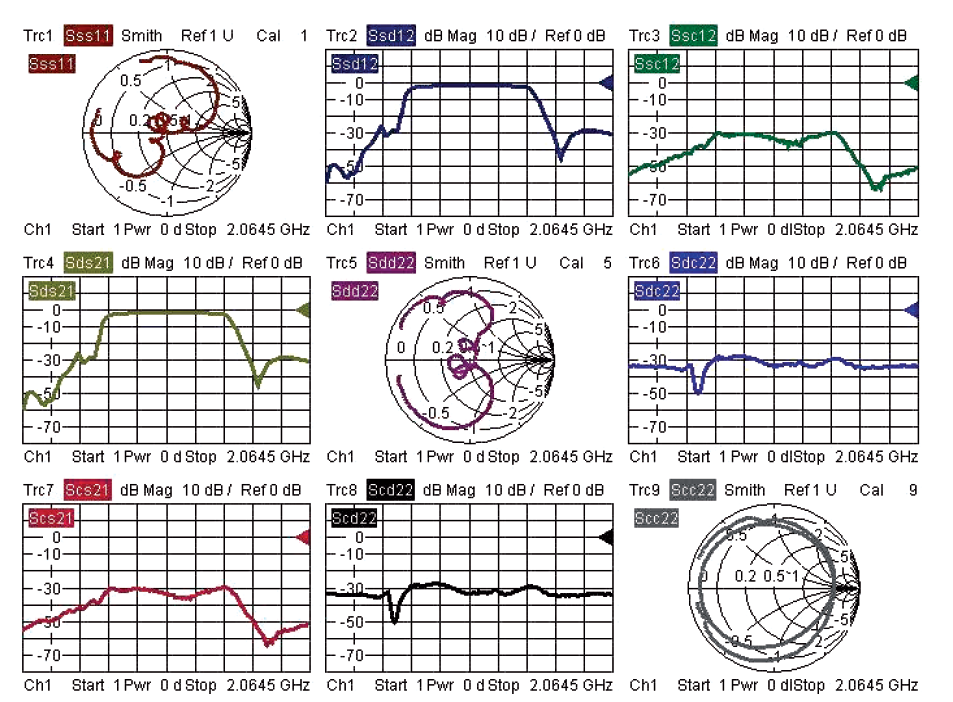
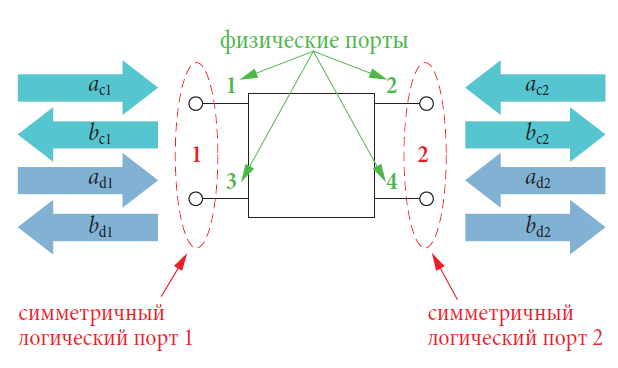
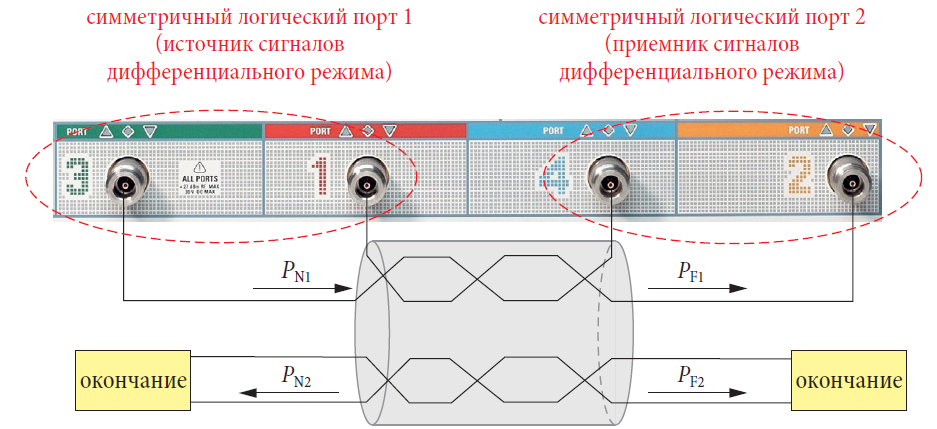
чистое различение между желательным сигналом и существующей помехой в форме синфазного сигнала больше невозможно. Когда оцениваются линии передачи и оборудование, используемое с ними, такое как системы разъемов, передатчики, приемники и т.д., то требуется измерение, которое позволяет раздельное наблюдение дифференциального и синфазного режимов и обеспечивает информацию о преобразовании режимов. Для целей характеризования используются волновые величины синфазного режима ac и bc и волновые величины дифференциального режима aд и bд. В каждом случае два физических порта комбинируются для формирования симметричного логического порта. Рис. 4.10.1 показывает пример симметричного двух-портового устройства.

1) Это также называется «дифференциальной» линией в технической литературе.

Нормально анализатор цепей имеет только односторонные коаксиальные1) порты, что означает, что он измеряет то, что известно как несимметричные S-параметры2), которые были определены в разделе 1.2. Используя подходяще сконфигурированные трансформаторы, эти тестовые порты могут быть адаптированы к симметричным ИУ. Поскольку физические трансформаторы имеют неудовлетворительные свойства (например, очень ограниченную полосу пропускания) анализатор моделирует идеальные трансформаторы, используя соответствующие модели цепей. Арифметический процесс, подобный встраиванию (см. раздел 4.8), интегрирует эти идеальные трансформаторы в цепочку обработки измерительных данных. Этот процесс известен как модальная декомпозиция.

1) В некоторых случаях они также называются небалансными в технической литературе.
2) В технической литературе также называемые «узловыми S-параметрами»

Большое преимущество этого процесса заключается в том, что не требуется никакого специального симметрирующего оборудования для измерений. Более того, можно использовать обычную технику калибровки и калибрационные стандарты. Современный анализатор цепей может автоматически выполнять модальную декомпозицию и пользователю только необходимо указать желаемые испытательные порты как симметричные порты. Результат измерений это так называемая S-матрица смешанного режима. Она характеризует соотношения между симметричными (балансными) волновыми величинами. Для симметричной двухпортовой цепи он имеет в общем 16 входов. Их значения проясняются, используя следующие измерительные примеры.

Пример 1. Конфигурация линии передачи для первого примера состоит из двух проводников с точно одинаковой длиной (электрическая длина 18,17 мм). Используемый анализатор цепей обеспечивает мастер измерений. На его первом шаге выбирается конфигурация тестового порта для симметричных измерений (см. следующий рисунок).

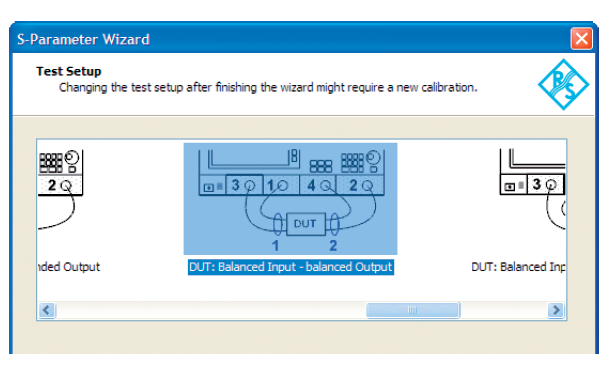
Оставшиеся диалоги Мастера измерений используются для конфигурирования частотного диапазона, полосы пропускания по ПЧ и выходной мощности испытательного порта. Здесь хорошо бы упростить прием предустановок по умолчанию. Как только мастер измерений сконфигурирован, выполняется калибровка и присоединяется ИУ. Анализатор цепей индицирует следующие результаты измерений (рис. 4.10.3):

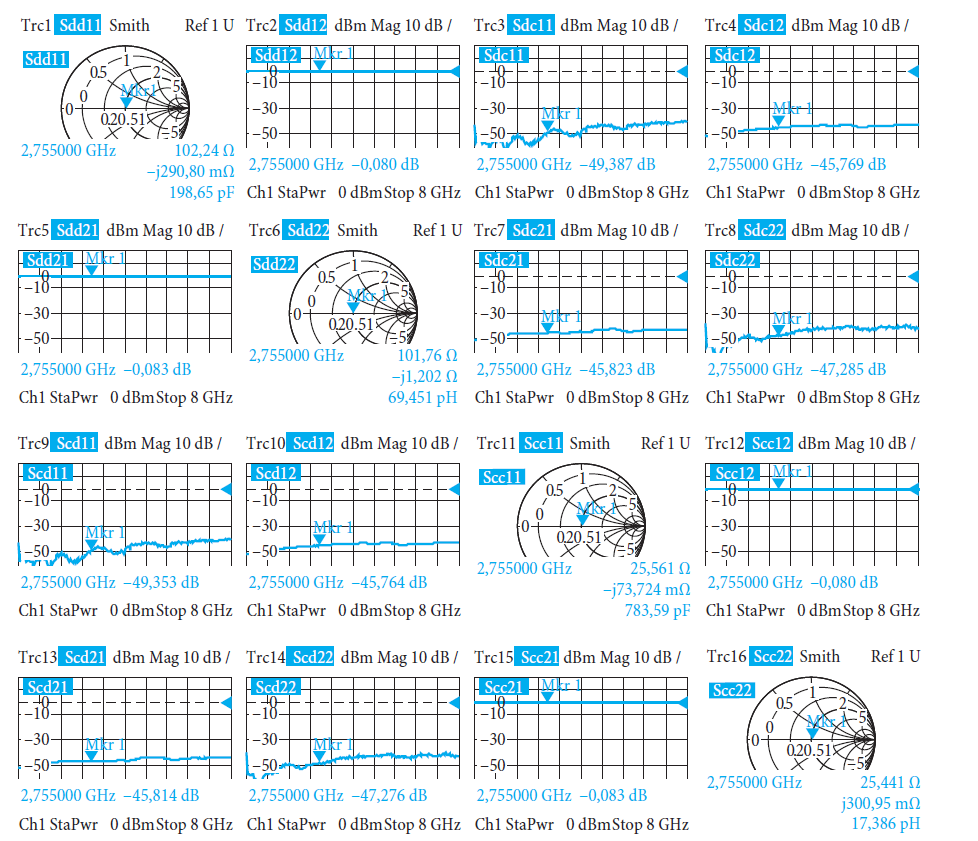
Графики на рис. 4.10.3 могут быть автоматически расположенными в соответствии со структурой модальной S-матрицы. Если мы используем эту структуру последовательно, это делает очень легким быстрое сравнение результатов измерений одного с другим, тем самым, сохраняя усилия на поиск между 16 откликами. Каждый S-параметр представляет отношение отраженной волны к падающей волне. Например, S-параметр sдc21 соответствует отношению bд2/ac1 (см. рис. 4.10.1). Индивидуальные S-параметры из измерений могут быть интерпретированы следующим образом:

◆◆ sдд11 ≈ sдд22 ≈ sдc11 ≈ sдc22 ≈ scд11 ≈ scд22 ≈ scc11 ≈ scc22 ≈ 0 Линия передачи завершается почти идеально. Никакой мощности не отражается в этом режиме и также между режимами.
◆◆ sдд12 ≈ sдд21 ≈ scc12 ≈ scc21 ≈ 1 Линия передает сигналы синфазного режима и дифференциального режима приблизительно без потерь между двумя симметричными портами.
◆◆ sдc12 ≈ sдc21 ≈ scд12 ≈ scд21 ≈ 0

В процессе передачи не возникает преобразования режима.

Пример 2. Во втором примере конфигурации линии передачи один из проводников удлиняется. Это означает, что проводники имеют электрические длины 18,17 мм и 72,80 мм, соответственно. В результате этой асимметрии меняются S-параметры смешанного режима.

Некоторые из графиков на рис. 4.10.4 имеют максимум или минимум на частоте f0 = 2,755 ГГц. Поведение ИУ может быть определено из S-параметров для измерений:

◆◆ sдд11 ≈ sдд22 ≈ sдc11 ≈ sдc22 ≈ scд11 ≈ scд22 ≈ scc11 ≈ scc22 ≈ 0 Как результат изменения длины, характеристические импедансы конфигурации линий передачи не модифицированы по сравнению с примером 1. Соответственно, примерное согласование все еще имеет место.
◆◆ sдд12, sдд21, scc12 и scc21 имеют грубо нулевое значение на f0 и
◆◆ sдc12, sдc21, scд12 и scд21 имеют грубо значение 1 на f0.

На частоте f0 удлинение линии передачи приводит к фазовому сдвигу в 180° между сигналами двух проводников. Подаваемые сигналы дифференциального режима полностью преобразуются в процессе передачи в синфазные сигналы. В сравнении с этим,
подаваемые сигналы синфазного режима полностью преобразуются в сигналы дифференциального режима. Соответственно, коэффициенты передачи смешанного режима sдc12, sдc21, scд12 и scд21 имеют значение грубо 1. Поскольку вся мощность, которая
поступает, преобразуется, то одномодовые коэффициенты передачи sдд12, sдд21, scc12 и scc21 имеют значение грубо 0.

4.11 Измерение перекрестных помех на ближнем и дальнем концах

Симметричные линии передачи могут состоять, например, из линий типа витой пары. В большинстве случаев, некоторые симметричные линии передачи организовываются в общие оболочки (или, по крайней мере, близко одна к другой). В дополнение к внешним помехам, обсуждавшимся в разделе 4.10, мы должны также учесть перекрестные (взаимные) помехи между парами линий. Различные величины вводятся для описания этих внутренних помех
в кабеле. Они базируются на правильном соотношении мощностей и относятся специально к дифференциальному режиму. При анализе перекрестных помех мы должны выбрать две пары проводников из кабеля и подключить их пассивные концы так, чтобы не возникало отражений. Для этой цели мы должны рассмотреть оба режима распространения, присутствующих в кабеле. Следующий рисунок показывает три реализации для такого подключения, свободного от отражений. ZCд называется характеристическим импедансом дифференциального режима, а ZCс – характеристическим импедансом синфазного режима линии передачи. Типовые значения, например, есть ZCд = 100 Ω и ZCс = 25 Ω.

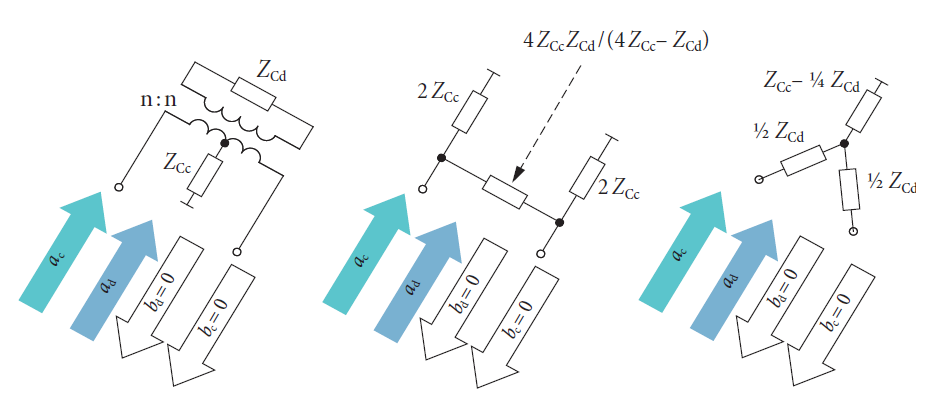
Источник, который используется, также является согласованным в обоих режимах линии передачи и возбуждает только дифференциальный режим одной пары проводников. Симметричные логические порты анализатора цепей могут быть использованы как волновой источник и приемник.

При измерении перекрестных потерь на ближнем конце dбл (NEXT) волновой источник и приемник присоединены к одному и тому же концу кабеля.

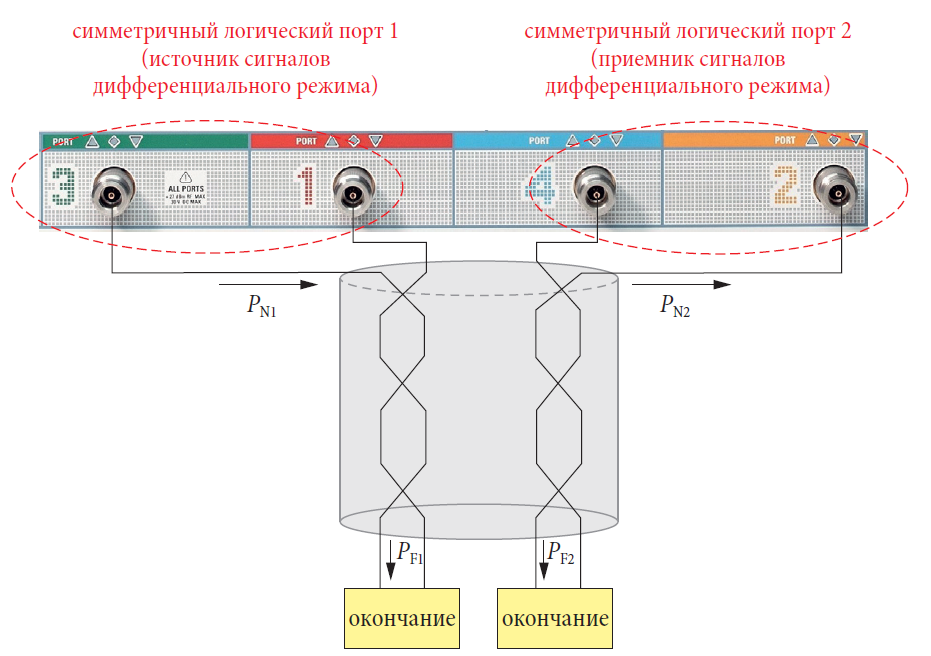
Источник обеспечивает волну дифференциального режима с доступной мощностью PN1. Приемник обнаруживает мощность перекрестной связи PN2 сигнала в дифференциальном режиме.

Из-за окончания на всех сторонах и того факта, что рассматривались сигналы только дифференциального режима, мощности PN1 и PN2 могут быть определены из компонентов PN1 = |aд1|2 и PN2 = |bд2|2, соответственно. Если мы используем организацию тестовых портов, показанную на рис. 4.11.2, мы можем также рассчитать dбл из параметра sдд21 измеренных значений, зафиксированных анализатором цепей.

Входные/выходные перекрестные потери на дальнем конце dдал,вх/вых (IOFEXT) определяются для подобной испытательной установки. Единственная разница заключается в том, что возбуждение и обнаружение выполняются с противоположных концов кабеля. Мощность возбуждения дифференциального режима дается выражением PN1. Приемник обнаруживает мощность PF2 (см. рис. 4.11.3).

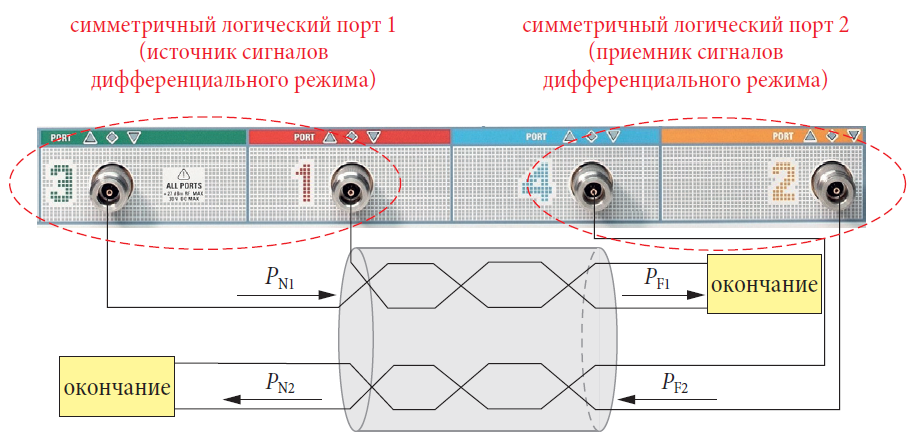
Здесь мы можем определить мощности в сравнении с предыдущим случаем, определяя PN1 = |aд1|2 и PF2 = |bд2|2. Если мы соединяем испытательные порты так, как показано на рис. 4.11.3, то dдал можно определить из параметра sдд21 измеренных значений, зафиксированных анализатором цепей.

В случае перекрестных потерь равного уровня на дальнем конце dдал,рав, обе мощности PF1 и PF2 измеряются на конце кабеля, который противоположен концу с возбуждением. Мощность PF2 называется мощностью, которая связана с помехой, как и в предыдущем случае.

В принципе, уровни мощности PF1 и PF2 могут быть определены, как и прежде, используя соответствующие волновые величины. Поскольку испытательная установка потребовала бы полных шести физических испытательных портов (симметричный источник и два симметричных приемника), мы обычно измеряем dдал,рав не напрямую. Чтобы выполнить это, нам необходимо знать потери кабеля dкаб, которые могут быть измерены, используя следующую испытательную установку:

Если мы соединяем тестовые порты, как это показано на рис. 4.11.4, dкаб, может быть также рассчитано из параметра sдд21 измеренных значений, зафиксированных анализатором цепей.

Мощность PF2 создается мощностью PN1 из-за механизма перекрестной связи. С другой стороны, мощность PF1 вызывается мощностью PN1 из-за потерь в кабеле dкаб. Следовательно, мы имеем следующее соотношение между величинами перекрестных потерь на дальнем конце:

4.12 Фильтр с симметричным и несимметричным портами, дисбаланс и подавление синфазного режима

В этом примере мы интересуемся фильтром на акустических поверхностных волнах (ПАВ-фильтр) с несимметричным портом 1 и балансным портом 2. Чтобы проверить работоспособность фильтра, он должен быть встроен в специальную согласующую цепь, которая реализуется, используя встраивание. По теории мы должны также реализовать согласующую цепь физически, используя подходящие компоненты. Однако, используя внедрение виртуальных цепей, мы не зависим от точности компонентов в согласующей цепи. Это является преимуществом, например, если нам необходимо сравнить результаты измерения от нескольких тестовых станций.

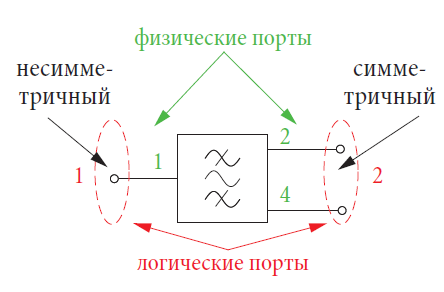
Сначала мы должны определить конфигурацию тестовых портов: логический порт 1 является несимметричным и соответствует физическому порту 1; логический порт 2 является симметричным и состоит из физических портов 2 и 4. Для симметричного порта выбраны дифференциальный опорный импеданс 75 Ω и синфазный опорный импеданс 25 Ω. Частотное качание отконфигурировано так, чтобы иметь центральную частоту 1, 9645 ГГц и размах 200 Мгц. Полоса пропускания измерения 1 кГц и выходная мощность испытательного порта 0 дБм являются подходящими. Все эти установки легко выполнить, например, с помощью Мастера измерений. На динамический диапазон можно воздействовать, изменяя выходную мощность испытательного порта и параметры полосы пропускания по ПЧ.

Блок автоматической калибровки используется для упрощения процесса калибровки. Как только подключено ИУ, определяется внедрение виртуальных цепей на логическом порту 2 с параллельной индуктивностью в 15 нГн.

Для центральной частоты графики на рис. 4.12.3 показывают коэффициент отражения scs11 ≈ 0 в порту 1 и коэффициент отражения дифференциального режима sдд22 ≈ 0 в порту 2. Это означает, что область пропускания показывает хорошее входное/выходное согласование для несимметричной и симметричной конфигурации, в которой используется фильтр. Коэффициент отражения синфазного режима scc22 в порту 2 в области пропускания соответствует более или менее полному отражению. Поскольку мощность обрезается как результат полного отражения в ИУ, этот режим не подходит больше для передачи. Коэффициенты передачи scs12 и scs21 для синфазных сигналов имеют поэтому очень низкие значения. Коэффициент передачи sдс21 характеризует передачу несимметричного сигнала из порта 1 в сигнал дифференциального режима в порту 2. Это является главной желательной функцией фильтра. Следовательно,
параметр sдs21 демонстрирует полосно-пропускающую характеристику фильтра. Величины sдс22 и sсд22 преобразование режима, которое возникает в результате отражения в порту 2. Обе они имеют очень маленькие значения, это является желательным, потому что это упрощает разделение синфазного и дифференциального сигналов в последующих частях цепи.

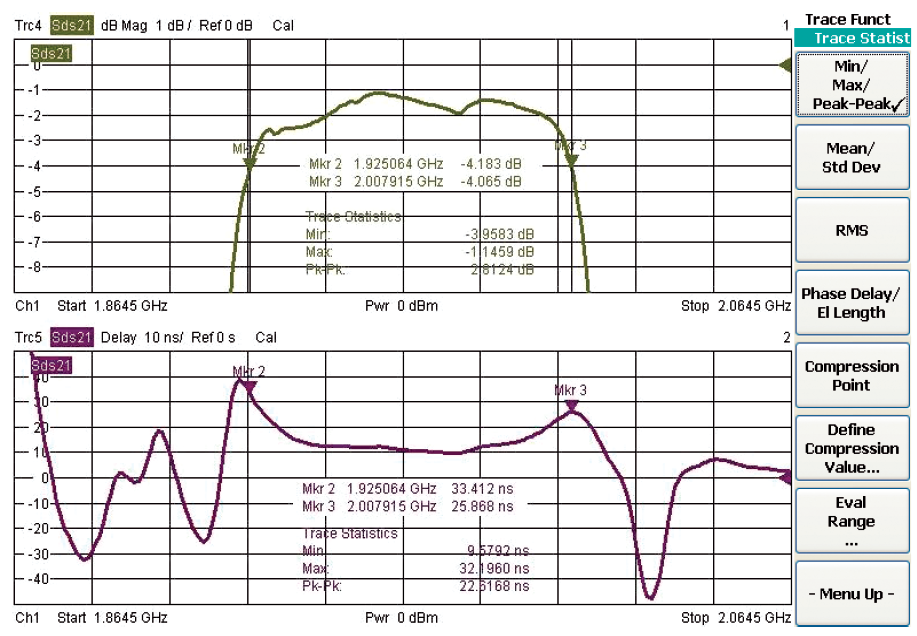
Теперь мы хотели бы проанализировать параметры sдs21 и scc11 более детально. Используя специальные маркерные функции, можно автоматически определять частоты отсечки по уровню 3 дБ, центральную частоту fц и Q фактор (добротность) графика sдs21 (см. рис. 4.12.4).

Чтобы считать простым образом согласование на частотных краях по уровню 3 дБ из scc11 и sдд22 из графики, можно использовать функцию связанных маркеров.

Используя статистические функции, можно оценить, например, пульсации графика. В этом процессе максимальное и минимальное значения рассчитываются вместе со средним значением для конкретного участка графика. В последующем мы хотели бы проанализировать пульсации амплитуды и группового запаздывания sсдs21. В этом примере полоса пропускания фильтра с его полосой в 3 дБ конкретизируется как диапазон оценивания статистической функции (см. рис. 4.12.5). Ширина шага апертуры должна быть определена эмпирически.

Для любого генерирования дифференциальных сигналов, подобного порту 2 фильтра, мы интересуемся, имеется ли коэффициент качества для сигнала дифференциального режима. Вот почему был введен термин дисбаланс (англ. Imbalance – IMB). Мы можем различать амплитудный дисбаланс aIMB и фазовый дисбаланс ΦIMB.

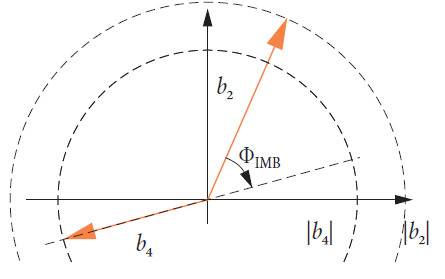
Амплитудный дисбаланс aIMB рассчитывается из отношения амплитуд несимметричных волн b2 и b4, которые формируют симметричный логический порт. Идеально, обе они имеют одинаковые амплитуды. Значения обычно указываются в дБ. С трех-портовым устройством (рис. 4.12.1) мы можем определить из несимметричных S-параметров s21 и s41.

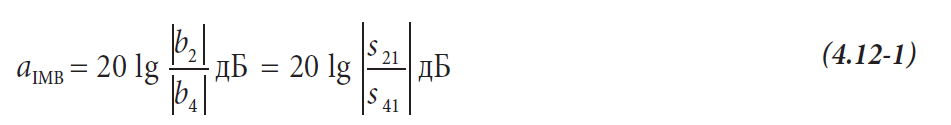
Фазовый дисбаланс ΦIMB характеризует отклонения фазы от идеального значения arg(b2) – arg(b4) = 180°. Для устройства, показанного на рис. 4.12.1, мы можем рассчитать ΦIMB из несимметричных S-параметров s21 и s41.

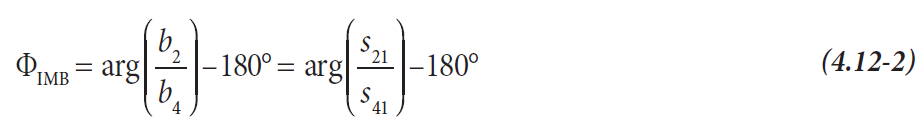
В дополнение, нам необходима величина, которая характеризует разницу между коэффициентом усиления по мощности синфазного режима Gc и коэффициентом усиления по мощности дифференциального режима Gд. Эта величина известная как коэффициент подавления синфазного режима (КПСР, в англ. CMRR).

Для цепи, показанной на рис. 4.12.1, коэффициент усиления по мощности дифференциального сигнала Gд измеряется между логическим портом 1 и логическим портом 2. Только мощность дифференциального сигнала рассматривается на симметричном логическом порту 2. Коэффициент усиления по мощности синфазного сигнала также измеряется между логическими портами 1 и 2, но только мощность синфазного сигнала рассматривается на симметричном логическом порту 2. Основываясь на измеренных величинах, показанных на рис. 4.12.3, можно рассчитать коэффициент подавления синфазного сигнала следующим образом:

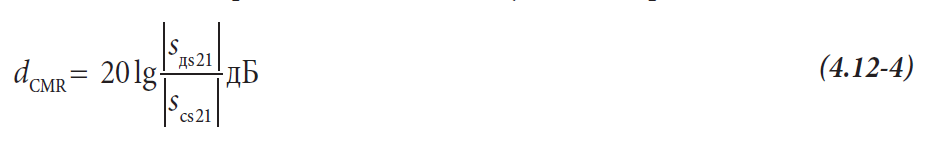
4.13 Измерение времени переключения и эффектов дрейфа

Электромеханические переключатели (ВЧ реле) иногда используются для переключения ВЧ сигналов. Они обычно шумно работают, и время переключения находится в диапазоне нескольких миллисекунд. Кроме такого решения, переключатели могут быть основаны на полевых транзисторах (например, переключатель на полевых транзисторах, переключатель на GaAs приборах). Они не имеют медленных механических приводных механизмов и могут
реагировать быстрее. Но они все-таки требуют времени на переключение, которое, главным образом, связано с эффектами заряда и разряда. В этом контексте, общей практикой является указывать время переключения, которое соответствует от 10 % до 90 % значения коэффициента передачи. Соответствующее время переключения обычно расположено в диапазоне до нескольких сотен наносекунд.

Измерение времени переключения с использованием внешнего запуска

Для характеризования времени переключения измеряется передача as21 или модуль коэффициента передачи |s21|, используя временное качание. На анализаторе включается режим внешнего запуска. Устройство запуска должно быть сконфигурировано так, чтобы точно одно качание запускалось бы от состояния устройства запуска. Сигнал запуска отводится как сигнал уровня 3,3 В транзисторно-транзисторной логики (TTL) и поступает через разъем EXT TRIGGER (внешний запуск) анализатора цепей. Используя цепь из резисторов, напряжение может быть адаптировано,как это требуется. В случае электромеханических переключателей отвод должен быть всегда организован в цифровой части контроллера переключателя. Сигнал, который следует прямо к электромеханическому приводному механизму, никогда не должен использоваться, поскольку он может создавать самонаведённое напряжение в процессе переключения. При некоторых обстоятельствах это напряжение может кратковременно достигать значения 100 В или больше. Это может вызвать неисправности в системе запуска ли даже повреждение анализатора цепей в самом плохом случае.

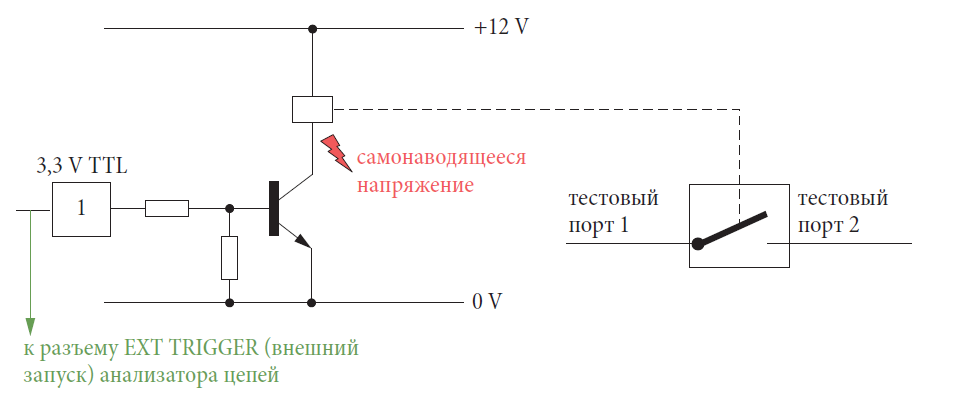
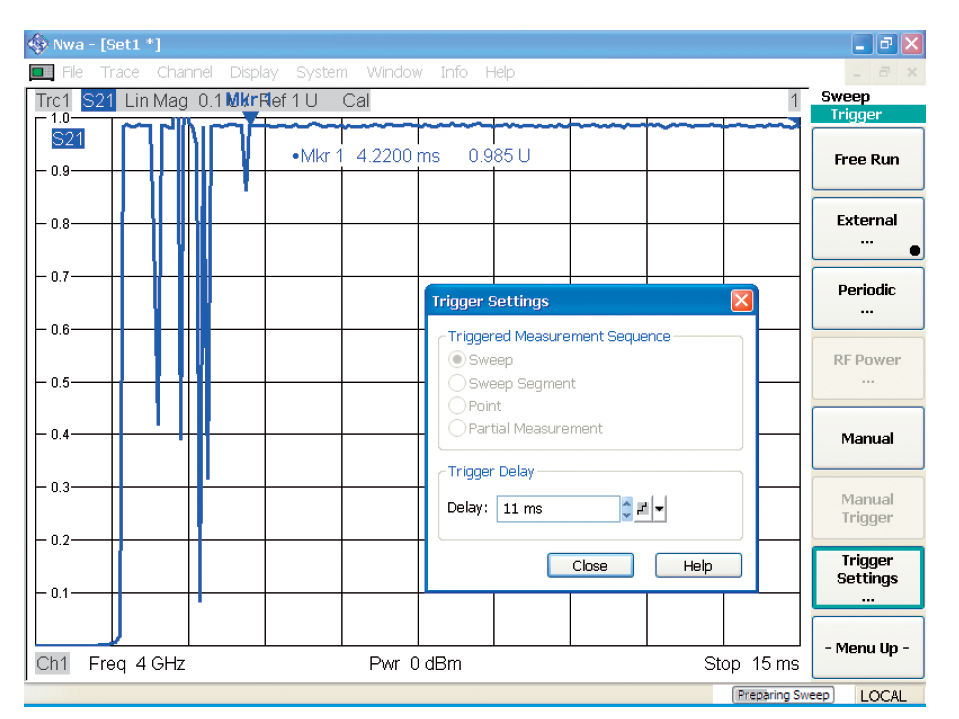
Рис. 4.13.2 показывает коэффициент передачи для ВЧ реле после того, как оно переключилось. Временная развертка была запущена, используя режим trigger delay (задержка запуска) в 11 мсек. В этом случае изменения в передаче могут наблюдаться очень легко, используя линейный масштаб по амплитуде. Щелчок переключателя является причиной статистических флуктуаций. Это делает необходимым измерение множества операций по переключению. Базируясь примерно на 25 измерениях, маркер 1 был установлен на значение времени, после которого никаких щелчков не ожидается.

Измерения дрейфа с использованием ВЧ запуска

В переключателях, основанных на полевых транзисторах, мы также интересуемся дрейфом переключателя. Мы можем наблюдать, например, запаздывание уровня от значения при 90 % до значения при 99,9 % величиной 120 мс. Измерение может быть запущено прямо от ВЧ сигнала, так что не требуется сигнала внешнего запуска. При измерении передачи s21 следует выбирать ВЧ уровень волновой величины b2. Порог запуска должен быть правильно адаптирован. При этом режиме запуска анализатор цепей контролирует ВЧ уровень и запускает развертку так скоро, как только конкретный порог запуска будет превышен.

Измерение дрейфа с использованием запуска от программного продукта

Не все анализаторы цепей имеют ВЧ запуск. Для рис. 4.13.3 и рис. 4.13.4 была выбрана временная развертка со временем свипирования 1 с. Был выбран режим ручного запуска. Используя программу, запущенную на внешнем компьютере, качание может запускаться и тогда, когда ИУ (переключатель на полевых транзисторах) включается. Это известно как асинхронный запуск. График (модуль и фаза) передается на внешний компьютер и тогда поведение ВЧ запуска моделируется, т.е. в данных графика выполняется поиск времени, за которое параметр s21 превышает конкретный порог, скажем, –30 дБ от первого времени. Данные графика перед этим временем отбрасываются. Оставшийся интервал наблюдения ограничен, скажем, 200 мс. Все графики на рис. 4.13.3 и рис. 4.13.4 нормированы к конечному значению в стационарном состоянии (здесь среднее последних 50 измеренных значений).

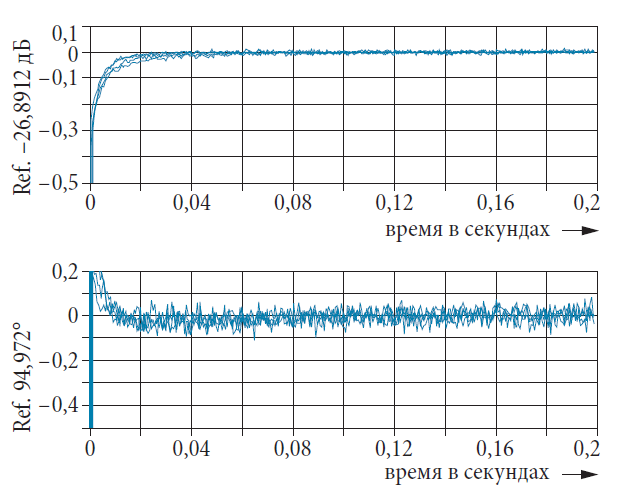
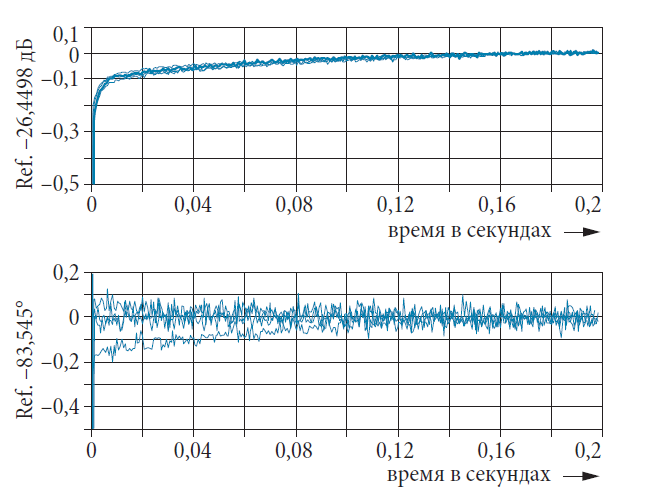
Одна проблема, которая возникает при анализе быстрых операций по переключению, заключается в том, что для анализатора цепей требуется время качания порядка 1 с, чтобы обработать временные флуктуации, которые имеют место при асинхронном запуске. Однако, анализаторы цепей, используемые в контексте настоящей книги, обеспечивают очень большое максимальное число точек измерения (20001 точку), так что разрешение порядка 0,05 мс между индивидуальными точками измерений может быть достигнуто вместе с подходящей полосой пропускания измерений. Это означает, что процессы с порядком величины 1 мс могут быть измерены без проблем, несмотря на время свипирования 1 с.

Программное обеспечение, необходимое для выполнения таких измерений, может быть записано, используя язык сценариев Matlab® из The MathWorks. Дистанционное управление тестовыми приборами, используя Matlab®, описано, например, в замечаниях по применению [1EF46]. Этот документ также описывает процедуру установки, необходимую для использования функции mexrsib. Следующая программа в кодах представляет одну возможную реализацию, которая основана на SCPI командах дистанционного управления для семейства анализаторов цепей, используемых здесь. Контроллер (персональный компьютер) соединяется с тестовым прибором через LAN (локальную сеть). Последовательный интерфейс компьютера (RS-232-C) используется для управления переключателем. Последовательный интерфейс обычно имеет 9-штырьковый Sub-D разъем и PIN 4 (Signal DTR) используется для включения и выключения переключателя. Время нарастания этого сигнала зависит от компьютера, который используется (в нашем случае 88 нсек). Напряжение сигнала DTR (типично –12 В или +12 В) должно быть адаптировано, используя соответствующие цепи. Тракт ВЧ измерений лежит между тестовыми портами 1 и 2 анализатора цепей.

4.14 Измерения усилителей, работающих в импульсном режиме

В области мобильных коммуникаций выходные усилители часто работают в режиме, который известен как импульсный рабочий режим. В GSM мобильном телефонном стандарте (Global System for Mobile Communications – Глобальная Система для Мобильных Коммуникаций) усилители работают в таймслоте длиной 577 мксек, который повторяется с периодичностью 8 таймслотов (4,616 мсек). Эти рабочие условия не могут быть изменены в процессе измерений, используя анализатор цепей по следующим причинам:

◆◆ Усилители обычно не проектируются для непрерывной работы. Они могут быть повреждены, если их время включения серьезно превышено.
◆◆ Мы хотели бы внимательно изучить поведение компонентов при реальных условиях работы.

Сигналы от функционального генератора включают и выключают ИУ. Выход SYNC (синхронизация) функционального генератора соединяется со входом EXT TRIGGER (внешний запуск) анализатора цепей. Режим внешнего запуска включается на анализаторе цепей. Он должен быть сконфигурирован таким образом, чтобы точно одна точка измерений регистрировалась на каждом цикле запуска. Это известно как точечный запуск. Реальное измерение выполняется как измерение передачи с использованием частотного качания. В нашем случае диапазон качания регулируется до частот GSM спутникового канала, т.е. от 1710 МГц до 1850 МГц (GSM 1800) или от 880 МГц до 960 МГц (GSM 900).

Задержка запуска в 100 мксек предотвращает от того, чтобы измерения выполнялись в то время, когда ИУ еще устанавливается в свое стационарное состояние. Полосы пропускания по ПЧ анализаторов должны выбираться так, чтобы время установления фильтра ПЧ было достаточно коротким, чтобы рабочий цикл выполнялся за оставшийся временной интервал. (В нашем случае мы рассчитали оставшееся время как 577 мксек – 100 мксек = 477 мксек).

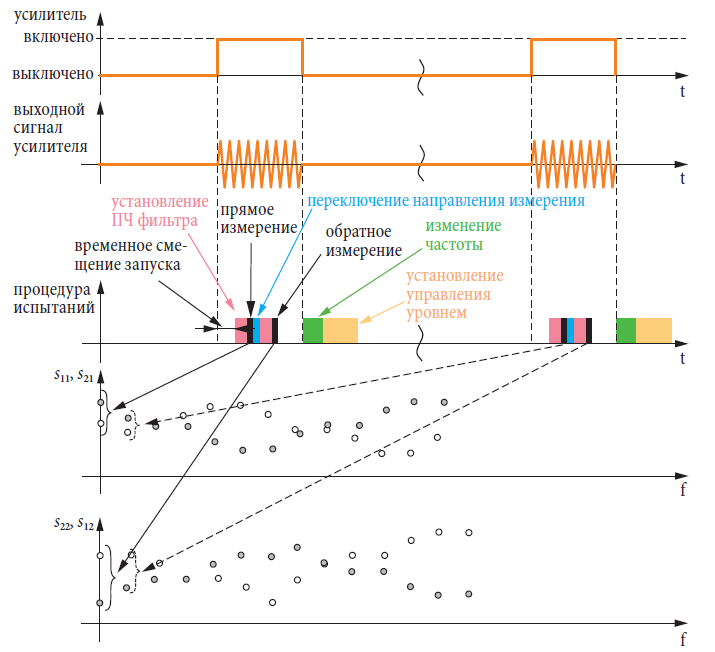
Поскольку одна точка измерений регистрируется каждые 4,616 мсек, качание, содержащее 201 точку потребует время качания около 928 мсек.

Полная двух-портовая калибровка обычно включается для этого измерения. Независимо от выбранного S-параметра, анализатором должны измеряться все двух-портовые S-параметры. Анализатор должен выполнять прямое и обратное измерения в пределах интервала времени 477 мксек. Необходимое время является суммой времени, требуемого для изменения направления плюс время установления ПЧ фильтра для каждого направления. Типичное время измерения тогда равно 82 мсек, если система автоматического управления уровнем выключена и используется полоса пропускания 100 кГц. В отличие от этого, время измерения величиной
31 мсек может достигаться без полной двух-портовой калибровки.

Некоторые анализаторы цепей также обеспечивают режим частичного запуска. Если выбран этот режим, то импульс запуска будет только запускать частичное измерение. Для определения частичного измерения, пожалуйста, обратитесь к разделу 2.7.1. Тогда изменение направления измерения может иметь место в паузы запуска (состояние OFF (выключено) усилителя на рис. 4.14.1). В этом случае, даже если включена коррекция системной ошибки, можно достичь время измерения примерно 31 мксек на каждый запуск. Однако, время качания тогда будет вдвое больше, скажем, 1855 мсек вместо 928 мсек.

4.15 Измерение эффективности (КПД)

Оборудование для мобильных радио применений, таких как мобильные телефоны, GPS приемники и т.д., главным образом, работают от батарей или перезаряжаемых элементов (аккумуляторов). Следовательно, низкая потребляемая мощность это одно из важнейших требований. Главный фактор для этого это ВЧ тракт, использующий усилители с высокой эффективностью.

Эффективность приращения мощности говорит нам о том, какая часть мощности, идущей к усилителю от источника питания реально преобразуется в ВЧ мощность. Преобразованная ВЧ мощность равна разности между выходной ВЧ мощностью и входной ВЧ мощностью ИУ (обычно усилителя).

Мощность, которая отражается входом усилителя из-за рассогласования, рассматривается как вклад в потери мощности. Для ВЧ входной мощности мы можем тогда предположить, что Pвч, вх = |a2|2. Выходная мощность есть мощность Pвч,вых = |b2|2, которая передается в согласованную нагрузку.

Из приведенных мощностей мы можем рассчитать эффективность (КПД) усилителя следующим образом:

В усилителях КПД η обычно зависит от входной мощности, рабочей частоты и температуры компонентов схемы. Используя частотное качание или качание по мощности, можно проанализировать эффективность как функцию некоторых различных параметров. Как общее правило, эффективность будет иметь максимум в окрестности точки 1 дБ-ной компрессии, в то время как она обычно уменьшается в диапазоне верхних рабочих частот усилителя.

Современные анализаторы цепей часто имеют активные испытательные порты (см. также раздел 2.4.3). Это дает возможность организовать источник постоянного питания через вход PORT BIAS (порт смещения) анализатора цепей, предполагая, что ИУ само не имеет собственной цепи DC смещения. Если анализатор цепей имеет пассивную испытательную установку, то DC связь должна быть обеспечена между точками смещения ИУ и тестовыми портами анализатора.

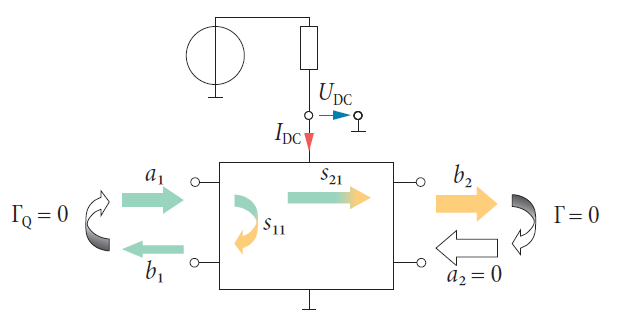
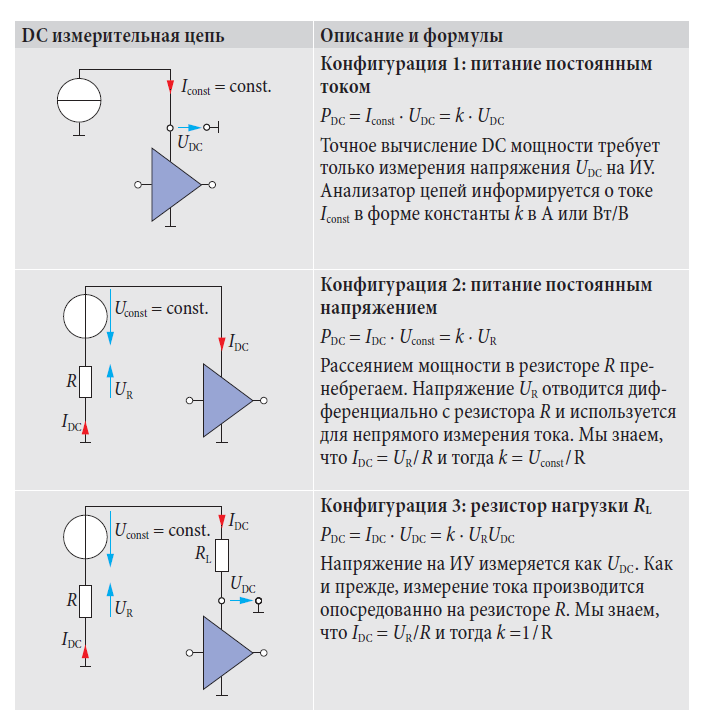
Анализатор цепей имеет специальные входы для измерений на постоянном токе (DC MEAS), чтобы измерять потребляемую испытываемым устройством DC мощность. Напряжение UDC может обычно прикладываться прямо к этим входам. Однако ток IDC должен измеряться опосредованно, как падение напряжения на прецизионном резисторе. С другой стороны, некоторые усилители поставляются с использованием источника постоянного тока. Численное значение тока тогда вводится в анализатор цепей, так что нет необходимости измерять ток. Подобная процедура может быть использована, если усилитель снабжен постоянным напряжением. Следующая таблица иллюстрирует несколько выбранных концепций источников питания вместе с их соответствующими измеренными величинами. Расчет константы k, требуемый анализатором цепей, также учтен.

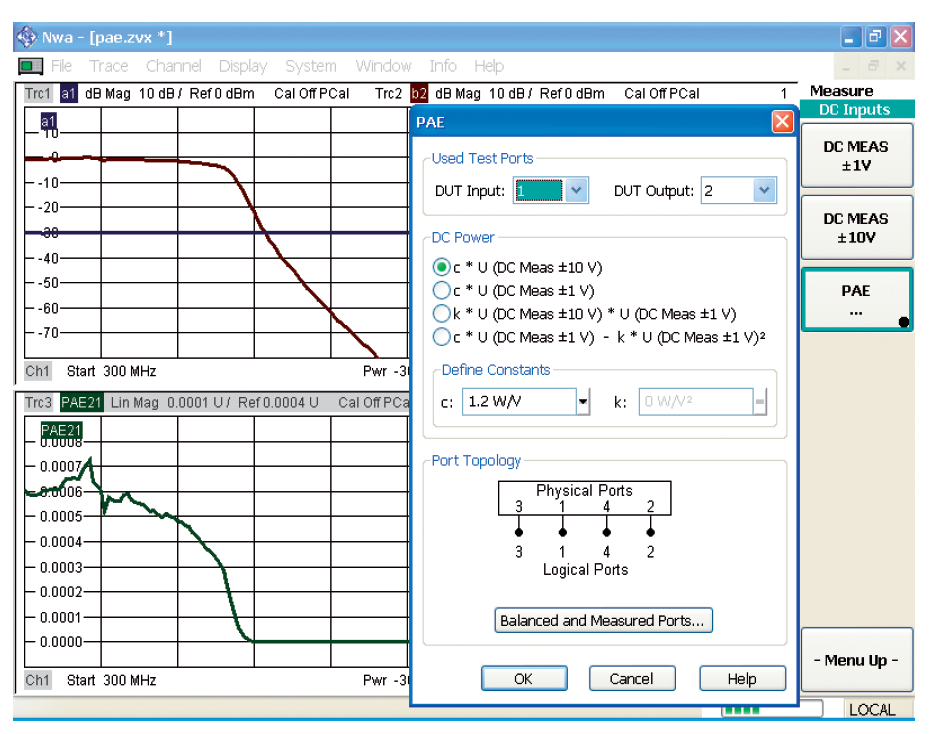
Следующий рисунок иллюстрирует измерение КПД для усилителя с сигналом низкой амплитуды. Конфигурация 2 была выбрана для использования в качестве нашей DC измерительной цепи. Качание частоты покрывает диапазон от 300 МГц до 3,3 ГГц. Используя калибровку мощности, были откалиброваны волновые величины a1 и b2, которые существенны в этом измерении. Из-за относительно низкой выходной мощности ИУ (1 мВт) и потребления мощности по DC приблизительно 1,5 Вт (126 мА при 12 В), была измерена эффективность менее, чем 0,1 %, в рабочем диапазоне частот (300 МГц до 1 Ггц).

Источник: www.rohde-schwarz.com/ru